Dimensionality Reduction

10/31/2022

Robert Utterback (based on slides by Andreas Muller)

\( \renewcommand{\vec}[1]{\boldsymbol{#1}} \newcommand{\E}{\mathop{\boldsymbol{E}}} \newcommand{\var}{\boldsymbol{Var}} \newcommand{\norm}[1]{\lvert\lvert#1\rvert\rvert} \newcommand{\abs}[1]{\lvert#1\rvert} \newcommand{\ltwo}[1]{\norm{#1}_2} \newcommand{\lone}[1]{\norm{#1}_1} \newcommand{\sgn}[1]{\text{sign}\left( #1 \right)} \newcommand{\e}{\mathrm{e}} \newcommand{\minw}{\min_{\vec{w} \in \mathbb{R}^p, b\in\mathbb{R}}} \newcommand{\summ}{\sum_{i=1}^m} \newcommand{\sumn}{\sum_{i=1}^n} \newcommand{\logloss}{\ln{(\exp{(-y^{(i)}(\vec{w}^T\vec{x}^{(i)}+b))} + 1)}} \newcommand{\ai}{\alpha^{(i)}} \newcommand{\w}{\vec{w}} \newcommand{\wt}{\vec{w}^T} \newcommand{\xi}{\vec{x}^{(i)}} \newcommand{\xit}{(\vec{x}^{(i)})^T} \newcommand{\xip}{\xit \vec{w}} \newcommand{\tip}{(\phi(\xi)^T \phi(\vec{x}))} \)

Dimensionality Reduction

Principal Component Analysis

A 2-dimensional input space
PCA finds the directions of maximum variance: the direction most elongated
Then look for the component that captures second-most variance, and so on
Returns an orthogonal basis (linear combinations of features with restrictions)
We could revisualize so that the components are our axes
That's what the transformed data is
So far just a rotation of input space
Color is not showing anything about the samples, it is just to show you where the data "goes" during the transformations
Since they're ordered by decreasing variance, we can drop some of these components
e.g., drop the second since it's not as important here
So we've gone from 2D to 1D
Kind of like the opposite of adding polynomial features: we're noticing when the dataset is actually in a lower dimensional space and reducing it down
We can then rotate back to the original space, which is basically removing some information

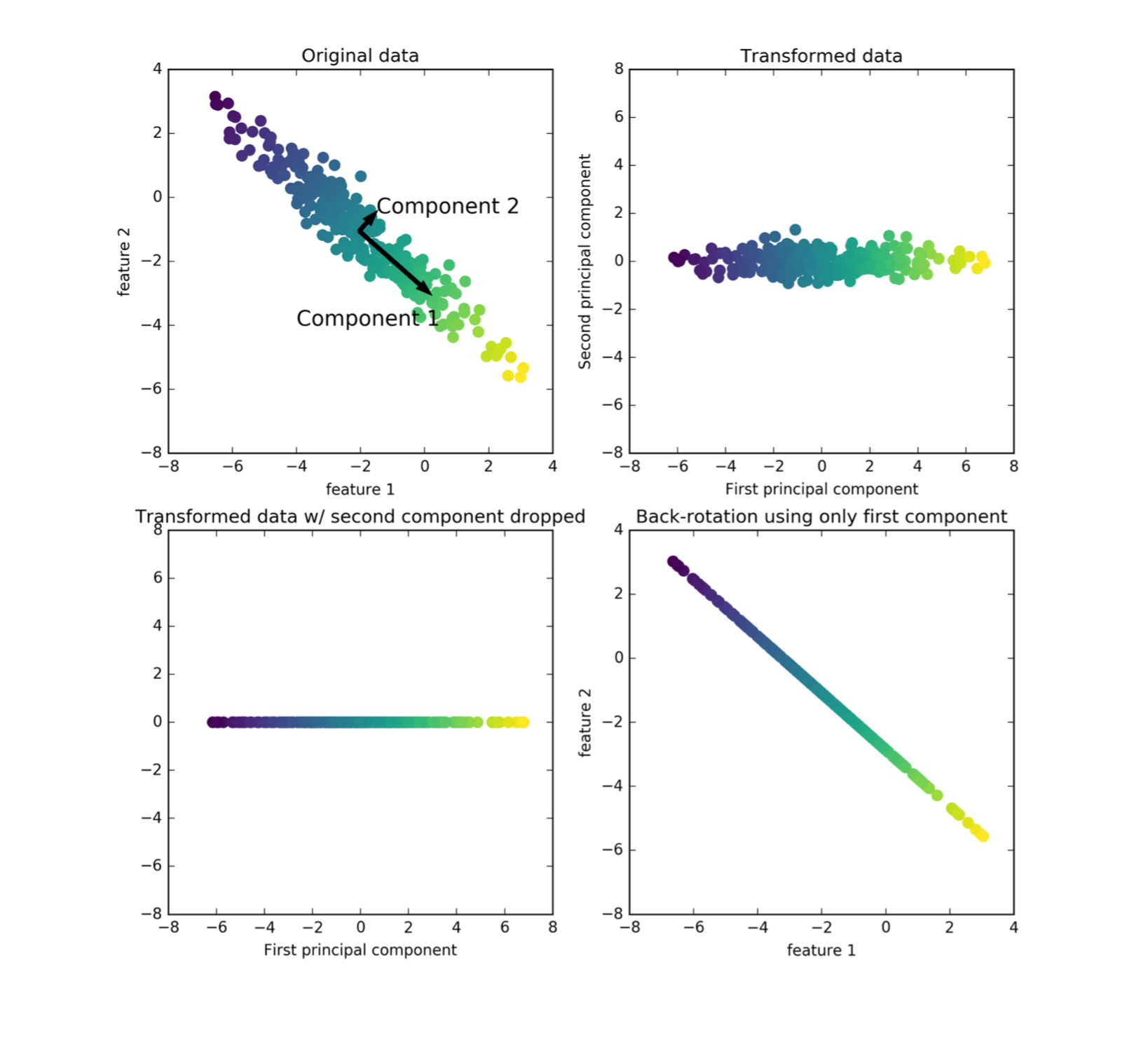
PCA objective(s)

\[\large\max\limits_{u_1 \in R^p, \| u_1 \| = 1} \text{var}(Xu_1)\] \[\large\max\limits_{u_1 \in R^p, \| u_1 \| = 1} u_1^T \text{cov} (X) u_1\]

PCA objective(s)

\[\large\min_{X', \text{rank}(X') = r}\|X-X'\|\]

PCA Computation

Center X (subtract mean).
In practice: Also scale to unit variance.
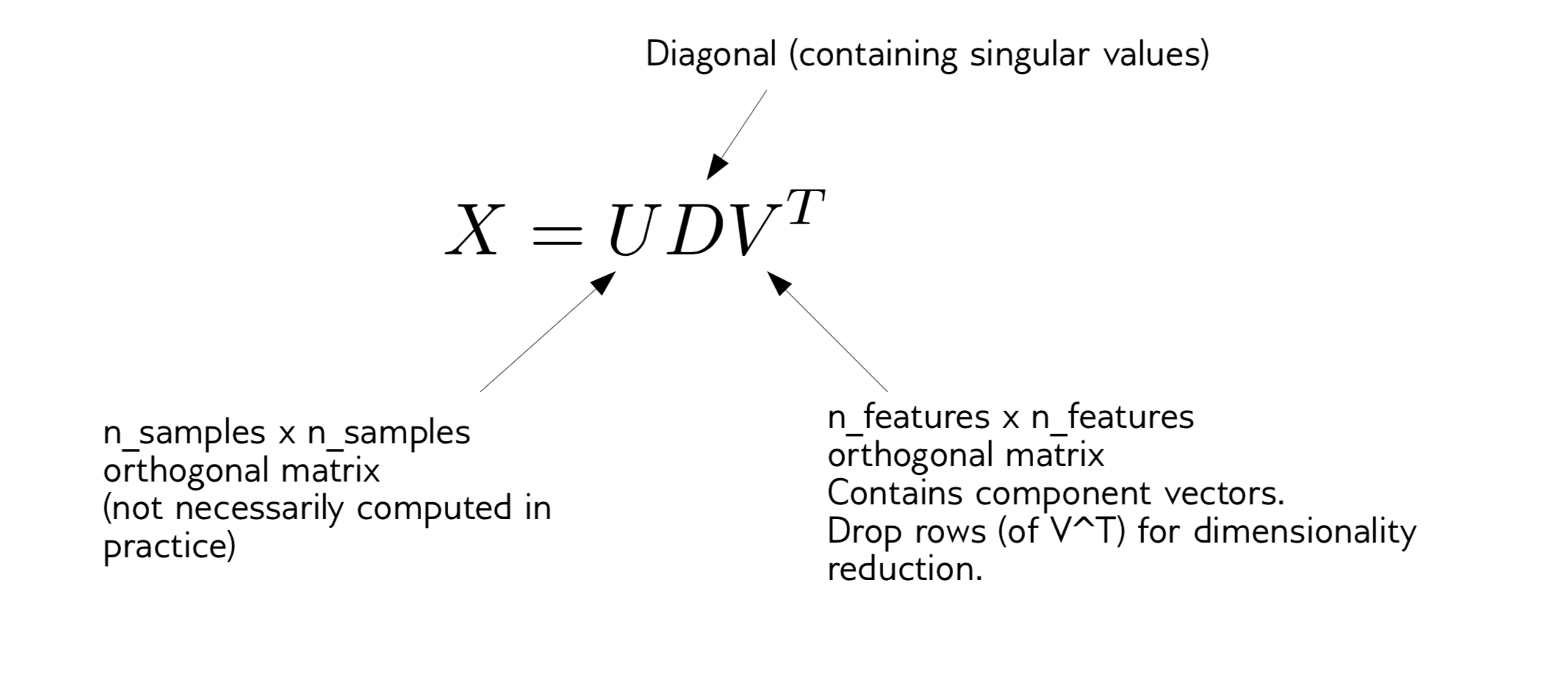
Compute singular value decomposition:

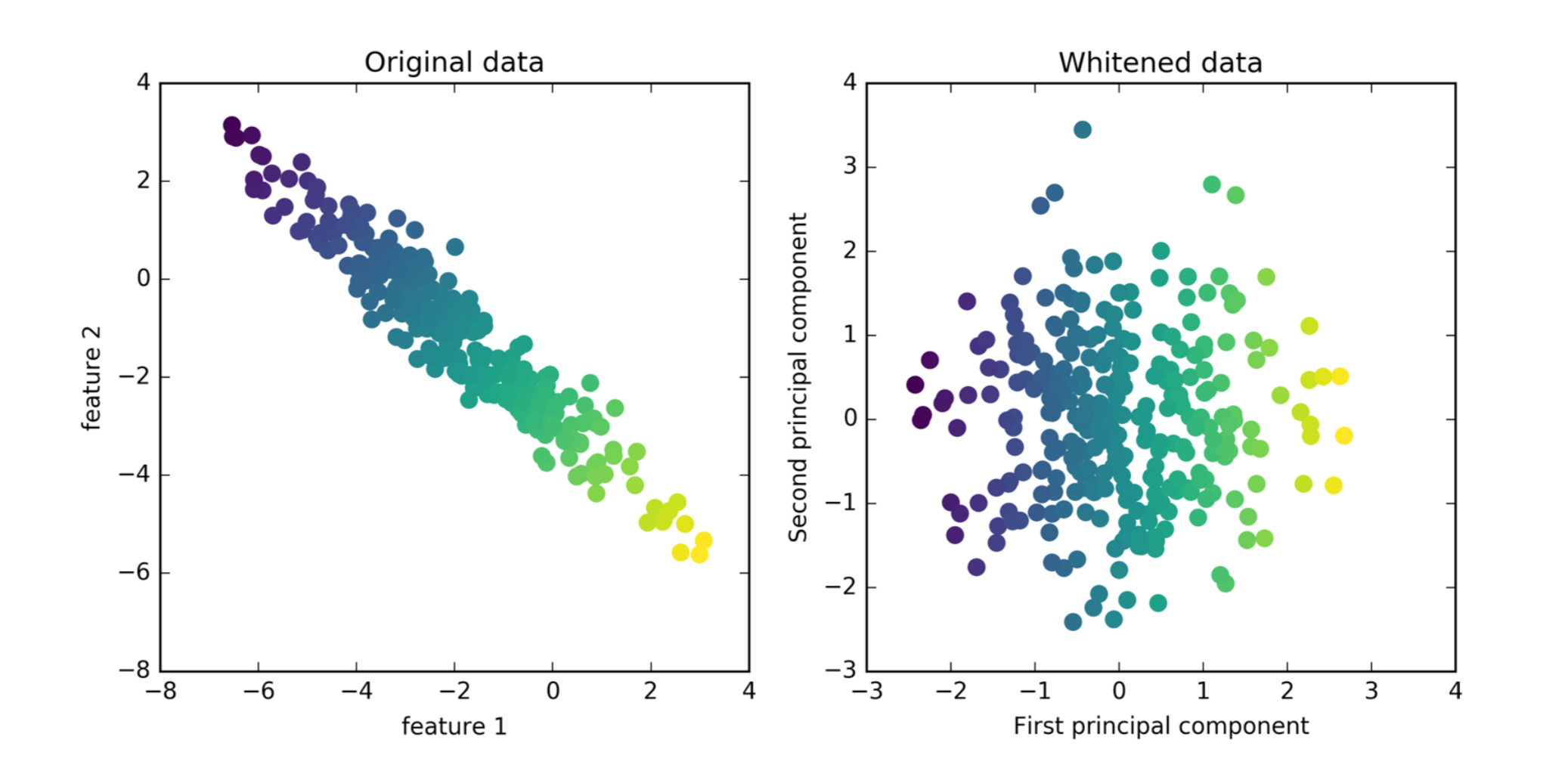
Whitening

Basically rotate data, then scale to stddev. 1
Same as using PCA without whitening, then doing StandardScaler.
You can see now the variance, visually looks like a ball, it was a Gaussian before. In the context of signal processing, in general, this is called whitening (white noise).
And if you want to use PCA as a feature transformation, to extract features you might want to do that, because otherwise, the magnitude of the first principal component will be much bigger than the magnitude of the other components since you just rotated it. So the small variance directions will have only very small variance because that's how you define them.
The question here is do you think the principal components are of similar importance? Or do you think the original feature is of similar importance?
And if you think the principal components are of similar important then you should do this. So if you want to go on and put this in a classifier, this might be helpful. But I don't think I can actually give you a clear rule when you would want to do this or when not to. But it kind of makes senses if you think of it as being centered scaler in a transformed space that seems like something that might be helpful for a classifier.

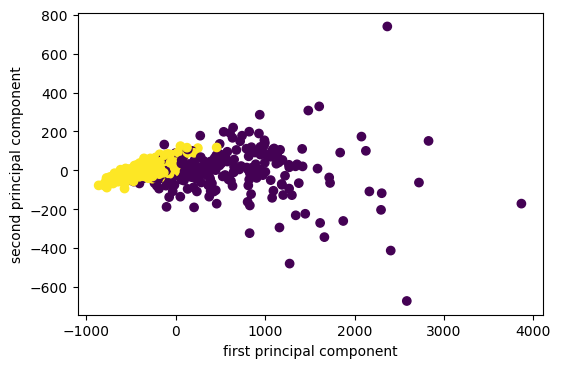
PCA for Visualization

from sklearn.decomposition import PCA
print(cancer.data.shape)
pca = PCA(n_components=2)
X_pca = pca.fit_transform(cancer.data)
# print(X_pca.shape)
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=cancer.target)
plt.xlabel("first principal component")
plt.ylabel("second principal component")
components = pca.components_
plt.imshow(components.T)
plt.yticks(range(len(cancer.feature_names)), cancer.feature_names)
plt.colorbar()

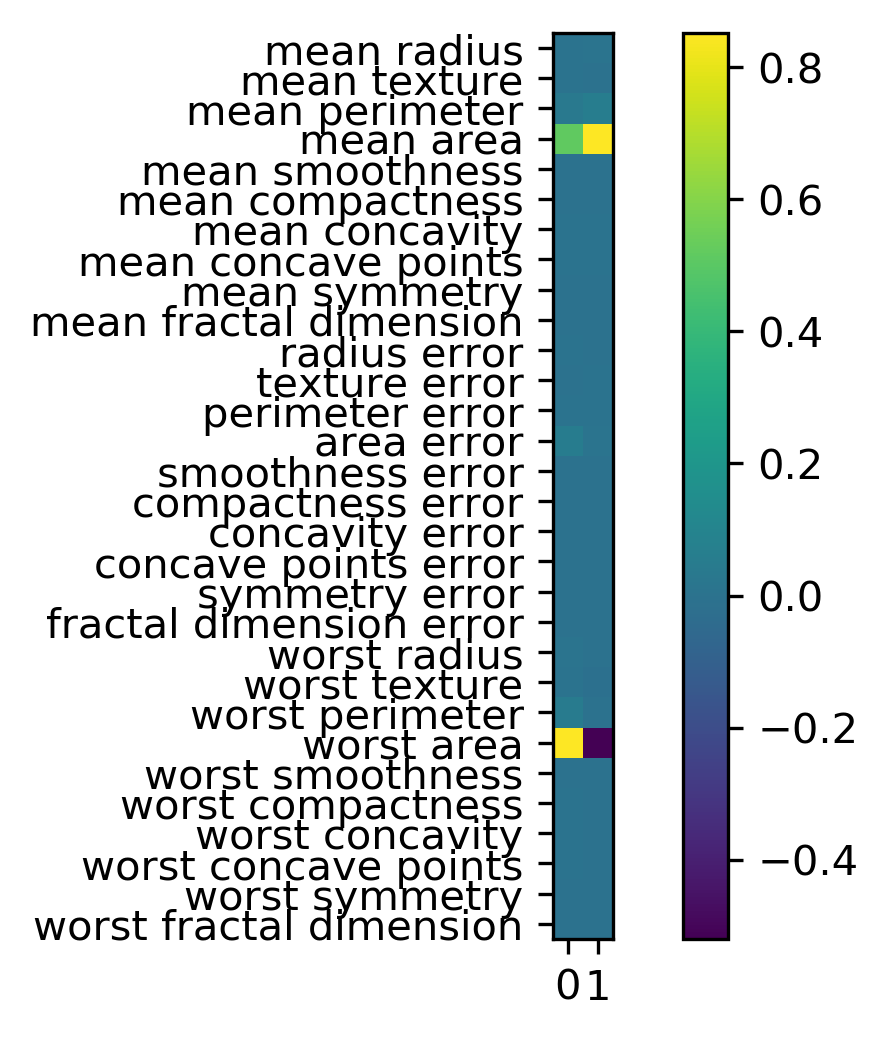
Scaling

pca_scaled = make_pipeline(StandardScaler(),
                       PCA(n_components=2),
                       LogisticRegression(C=10000))
pca_scaled.fit(X_train, y_train)
print(pca_scaled.score(X_train, y_train))
print(pca_scaled.score(X_test, y_test))

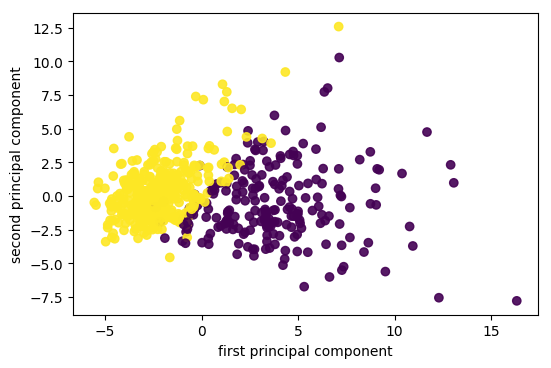
Inspecting Components

components = pca_scaled.named_steps['pca'].components_
plt.imshow(components.T)
plt.yticks(range(len(cancer.feature_names)),
           cancer.feature_names)
plt.colorbar()

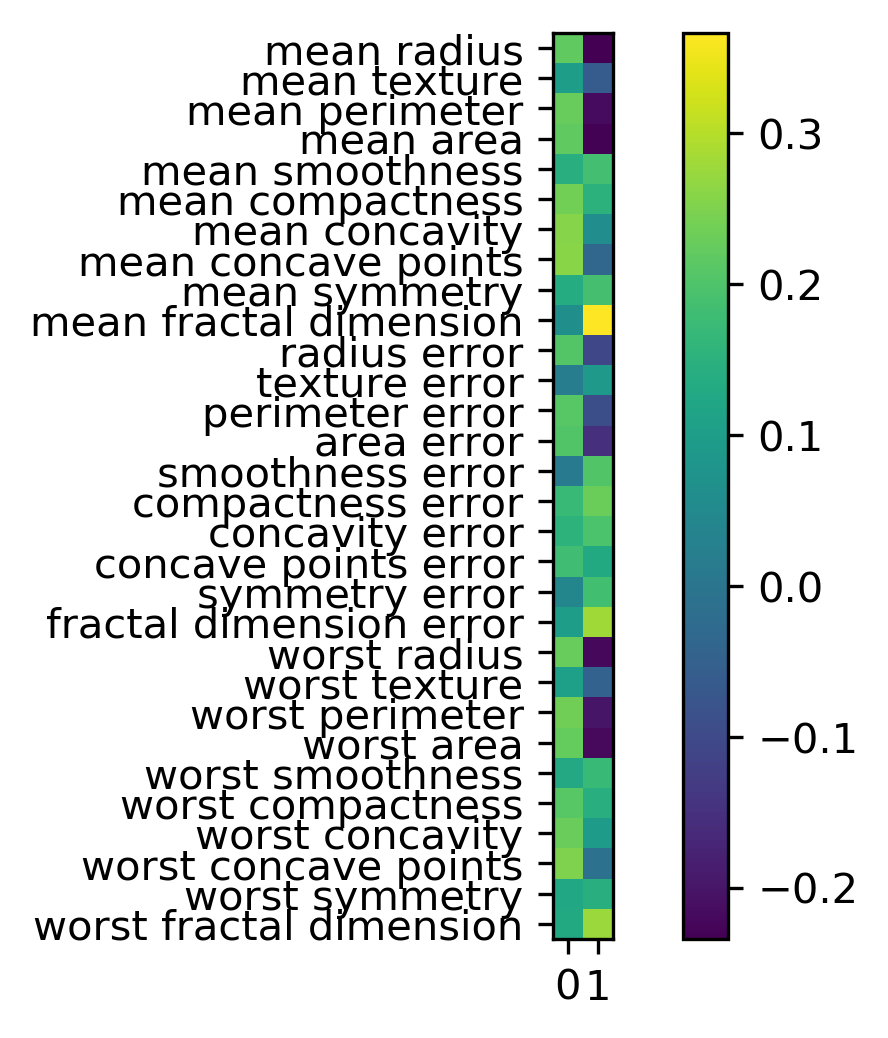
PCA for Regularization

X_train, X_test, y_train, y_test = \
    train_test_split(cancer.data, cancer.target,
                     stratify=cancer.target, random_state=0)
lr = LogisticRegression(C=10000, solver='liblinear')
lr.fit(X_train, y_train)
print(f"{lr.score(X_train, y_train):.3f}")
print(f"{lr.score(X_test, y_test):.3f}")

0.984
0.930

from sklearn.decomposition import PCA
lr = LogisticRegression(C=10000, solver='liblinear')
pca_lr = make_pipeline(StandardScaler(),
                       PCA(n_components=2), lr)
pca_lr.fit(X_train, y_train)
print(f"{pca_lr.score(X_train, y_train):.3f}")
print(f"{pca_lr.score(X_test, y_test):.3f}")

0.960
0.923

Variance Covered

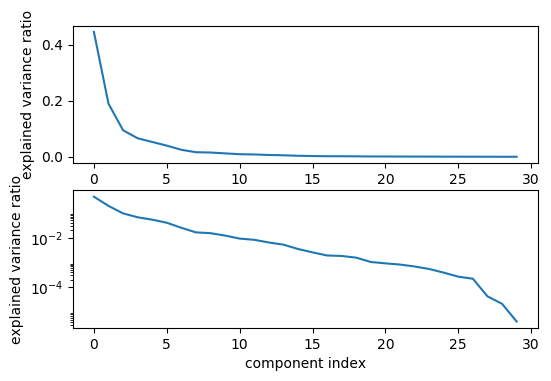
pca_lr = make_pipeline(StandardScaler(),
                       PCA(n_components=6), lr)
pca_lr.fit(X_train, y_train)
print(f"{pca_lr.score(X_train, y_train):.3f}")
print(f"{pca_lr.score(X_test, y_test):.3f}")

0.981
0.958

Interpreting Coefficients

pca = pca_lr.named_steps['pca']
lr = pca_lr.named_steps['logisticregression']
coef_pca = pca.inverse_transform(lr.coef_)

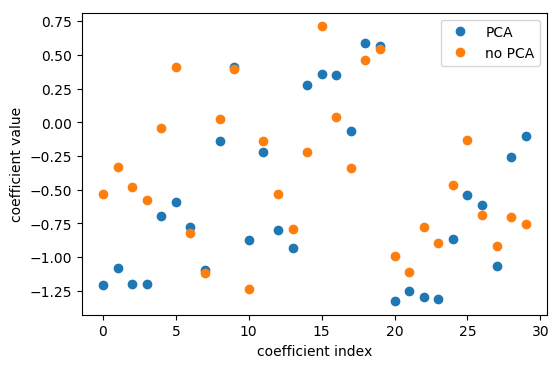
PCA+logreg.png

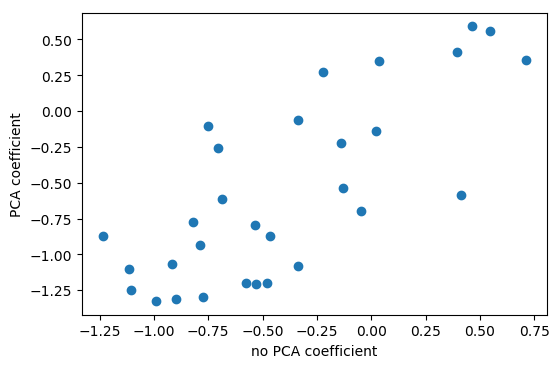
logreg+noPCA.png

PCA is Unsupervised!

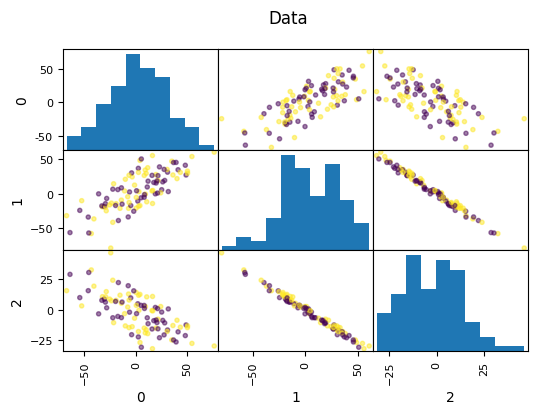
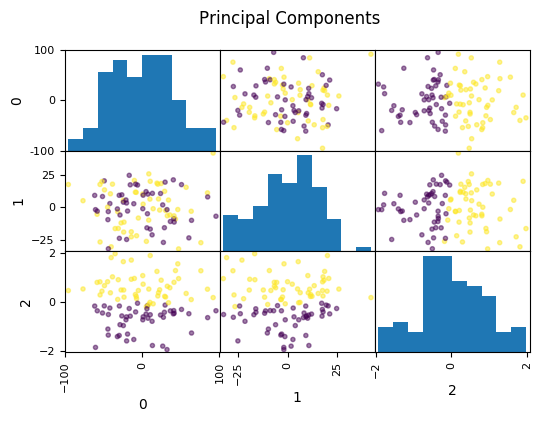
PCA for Feature Extraction

We can also "extract" features
Used to be very popular in images of faces
Though deep learning has kind of taken over this kind of thing
So we have a bunch of faces
And we want to detect who a particular face is
Naive: use the pixel space as inputs, i.e., the value of each pixel
That would be VERY high dimensional and probably wouldn't work very well
Instead we use PCA to find groups of pixels that are important together
And what you get are these new features, that kind of represent various facial features
Some of these heads are tilted left or right, some downward facing, etc.
Some of it is also which direction does the light come from, darkness of eyebrows, etc.
Each face picture is a linear combination of the PCA components, weighted by the coefficients that a model learns
So is a person's face is facing left, you expect that component coefficient to be high
So this is kind of cool, but again, this doesn't necessarily make good classifications
So the first two seem to be able which side the light comes from, which is an interesting feature of the picture but NOT of the face…

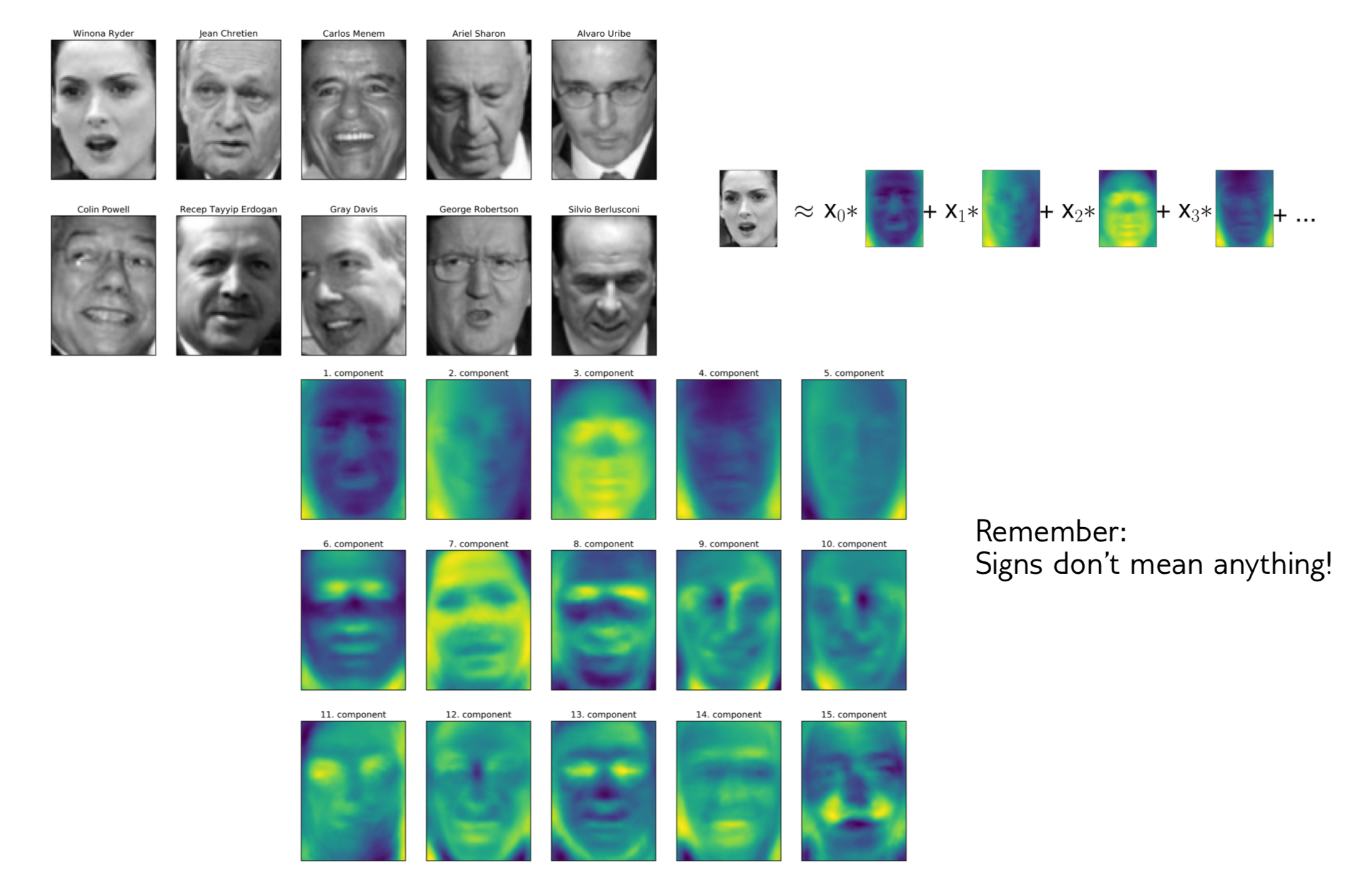
1-NN and Eigenfaces

from sklearn.datasets import fetch_lfw_people
from sklearn.neighbors import KNeighborsClassifier
people = fetch_lfw_people(min_faces_per_person=35, resize=0.7)
X_people, y_people = people.data, people.target

X_train, X_test, y_train, y_test = \
    train_test_split(X_people, y_people,
                     stratify=y_people, random_state=0)
print(X_train.shape)
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train, y_train)
print(f"{knn.score(X_test, y_test):.3f}")

(1539, 5655)
0.311

pca = PCA(n_components=100, whiten=True, random_state=0)
pca.fit(X_train)
X_train_pca = pca.transform(X_train)
X_test_pca = pca.transform(X_test)
print(X_train_pca.shape)


>>> (1539, 100)

knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(X_train_pca, y_train)
print(f"{knn.score(X_test_pca, y_test):.3f}")

0.331

Reconstruction

PCA for Outlier Detection

pca = PCA(n_components=100).fit(X_train)
inv = pca.inverse_transform(pca.transform(X_test))
reconstruction_errors = np.sum((X_test - inv)**2, axis=1)

Best reconstructions

Worst reconstructions

Manifold Learning

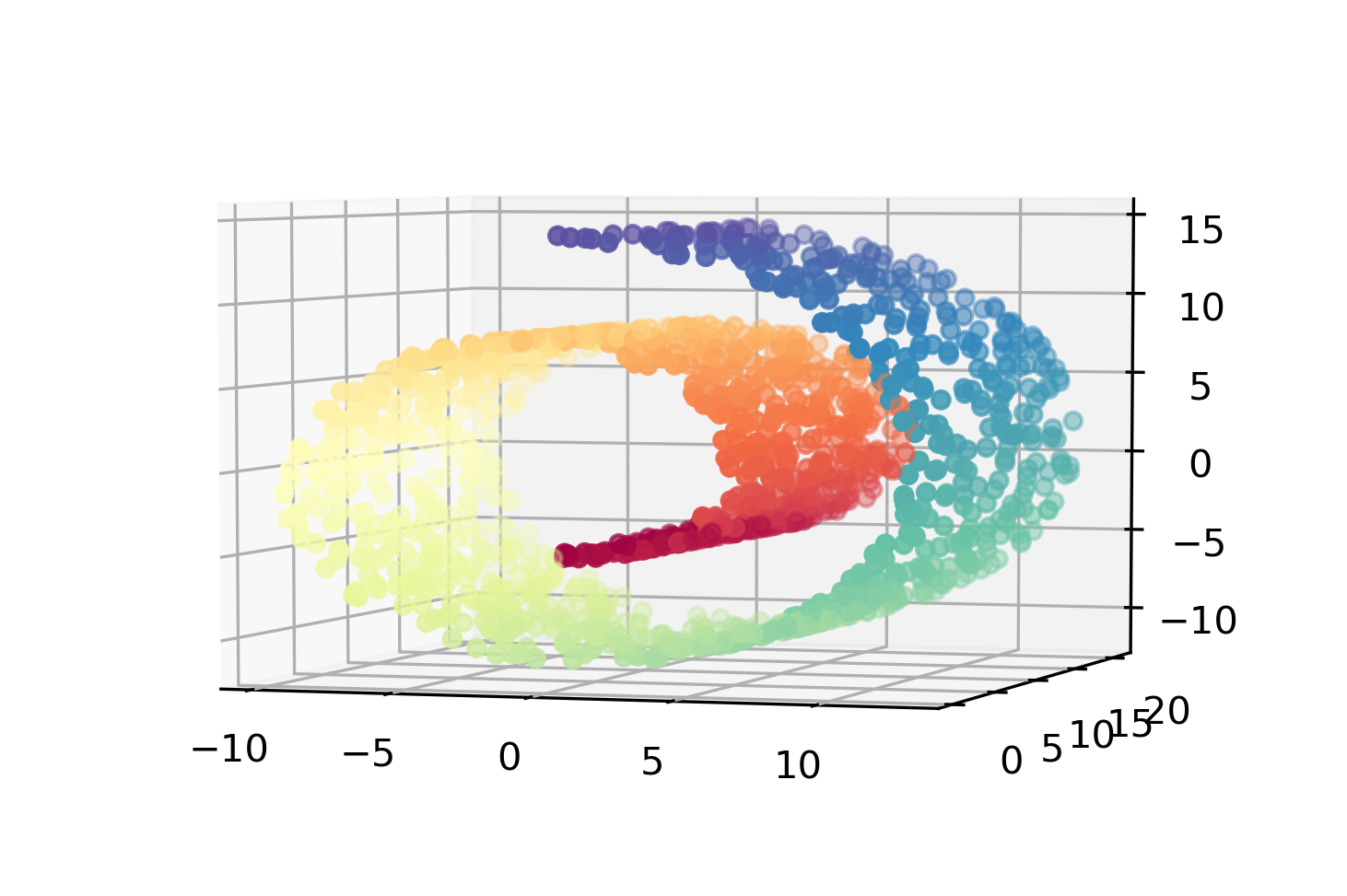
Pros and Cons

For visualization only
Axes don’t correspond to anything in the input space.
Often can’t transform new data.
Pretty pictures!

Algorithms in sklearn

KernelPCA – does PCA, but with kernels
- Eigenvalues of kernel-matrix
Spectral embedding (Laplacian Eigenmaps)
- Uses eigenvalues of graph Laplacian
Locally Linear Embedding
Isomap “kernel PCA on manifold”
t-SNE (t-distributed stochastic neighbor embedding)

t-SNE

\[p_{j\mid i} = \frac{\exp(-\lVert\mathbf{x}_i - \mathbf{x}_j\rVert^2 / 2\sigma_i^2)}{\sum_{k \neq i} \exp(-\lVert\mathbf{x}_i - \mathbf{x}_k\rVert^2 / 2\sigma_i^2)}\]\[p_{ij} = \frac{p_{j\mid i} + p_{i\mid j}}{2N}\]

\[q_{ij} = \frac{(1 + \lVert \mathbf{y}_i - \mathbf{y}_j\rVert^2)^{-1}}{\sum_{k \neq i} (1 + \lVert \mathbf{y}_i - \mathbf{y}_k\rVert^2)^{-1}}\]

\[KL(P||Q) = \sum_{i \neq j} p_{ij} \log \frac{p_{ij}}{q_{ij}}\]

Main idea: find a probability distribution over your data points
given one data point, if I pick one neighbors at random but weighted by distance, how likely to pick neighbor j
Intuitively, for each data point, look at the density of the neighbors
Make symmetric
It's a distribution over pairs of points
Then assume we have some embedding, those are the y points (x are original)
Look at a similar thing but distance between the ys
What we want is for these two distributions to be the same
So we try to minimize the bottom thing
—
Starts with a random embedding
Iteratively updates points to make "close" points close. (gradient descent)
Global distances are less important, neighborhood counts.
Good for getting coarse view of topology.
Can be good for finding interesting data point
t distribution heavy-tailed so no overcrowding.
(low perplexity: only close neighbors – hyperparameter)

from sklearn.manifold import TSNE
from sklearn.datasets import load_digits
digits = load_digits()
X = digits.data / 16.
X_tsne = TSNE().fit_transform(X)
X_pca = PCA(n_components=2).fit_transform(X)

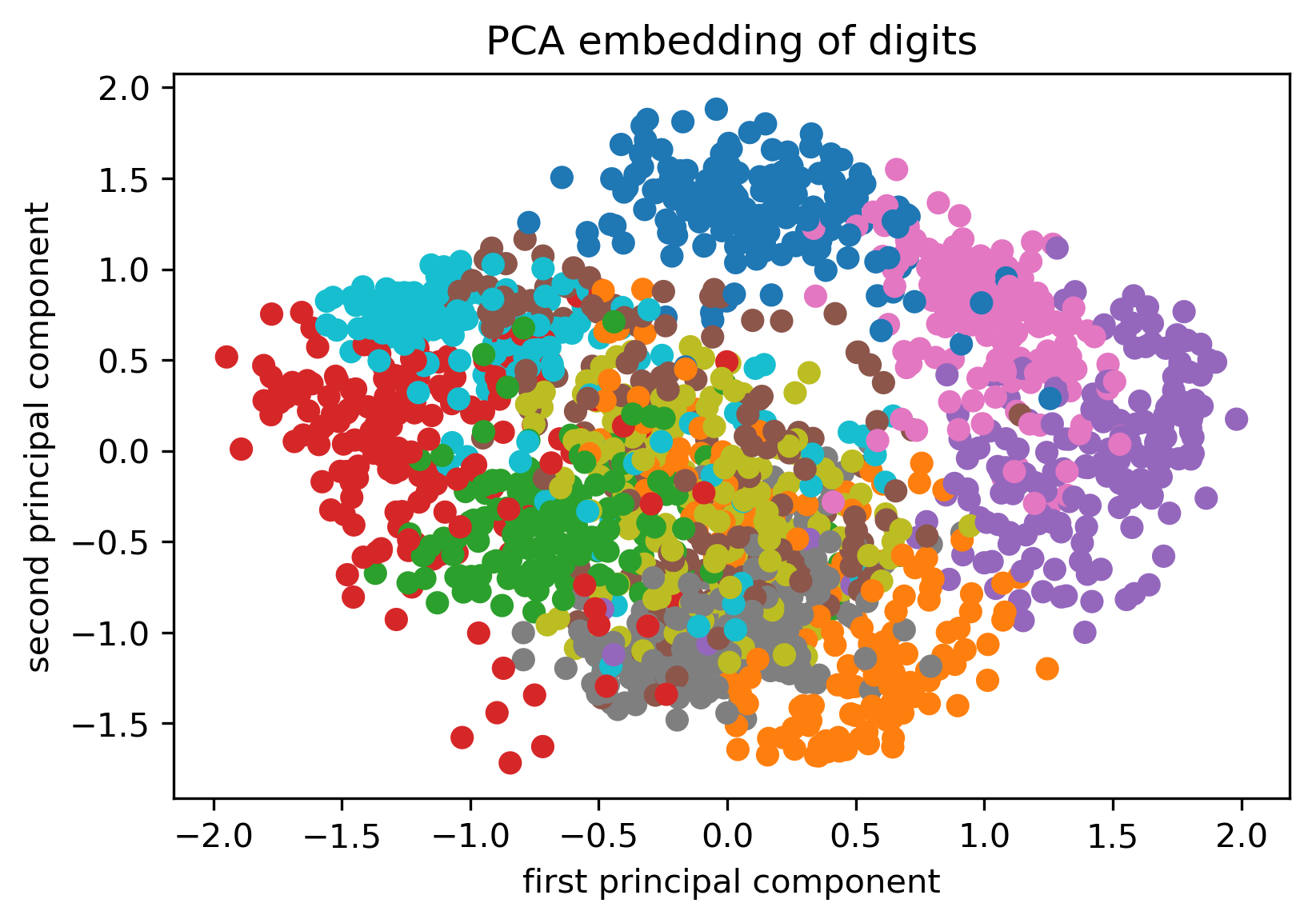
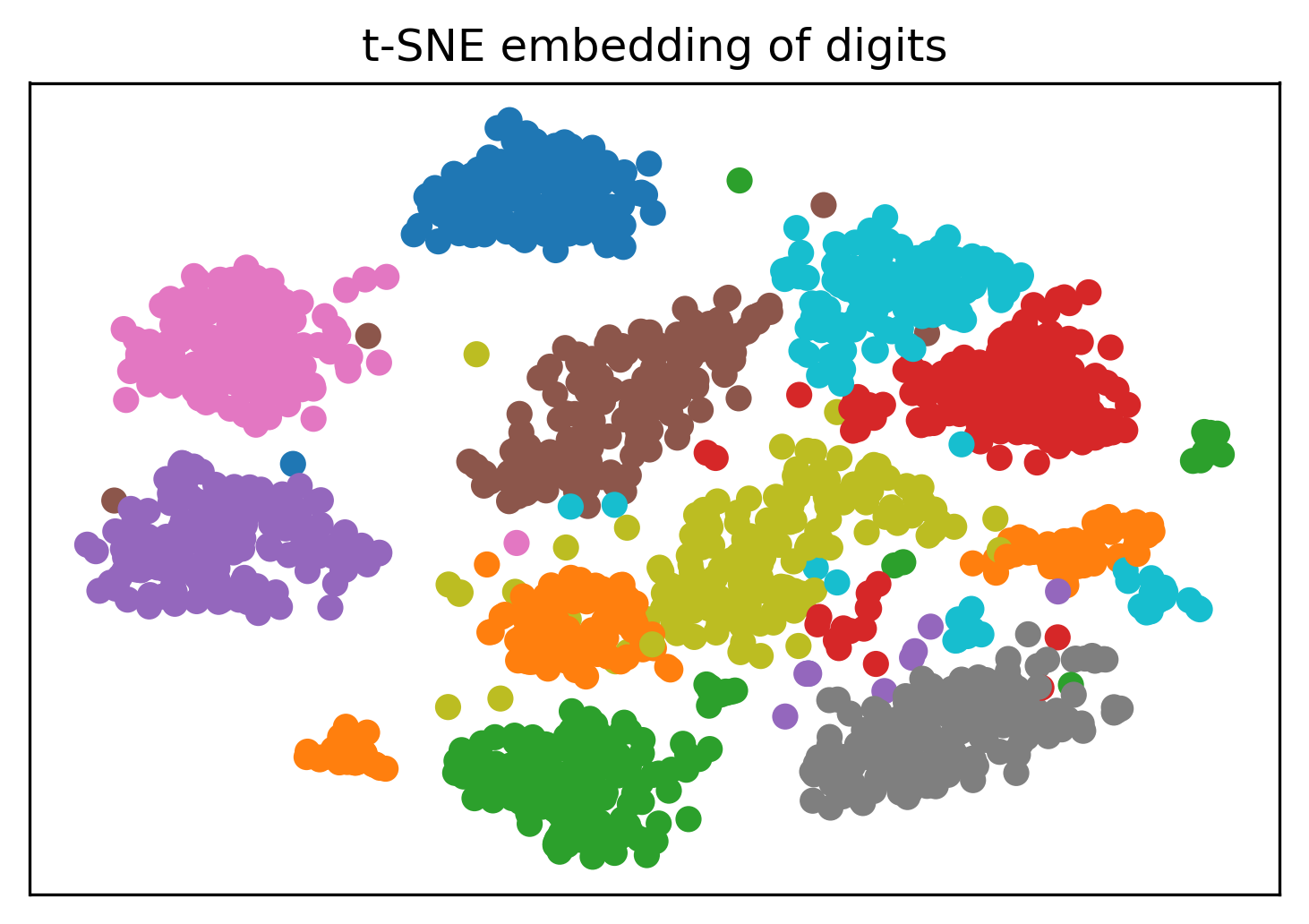
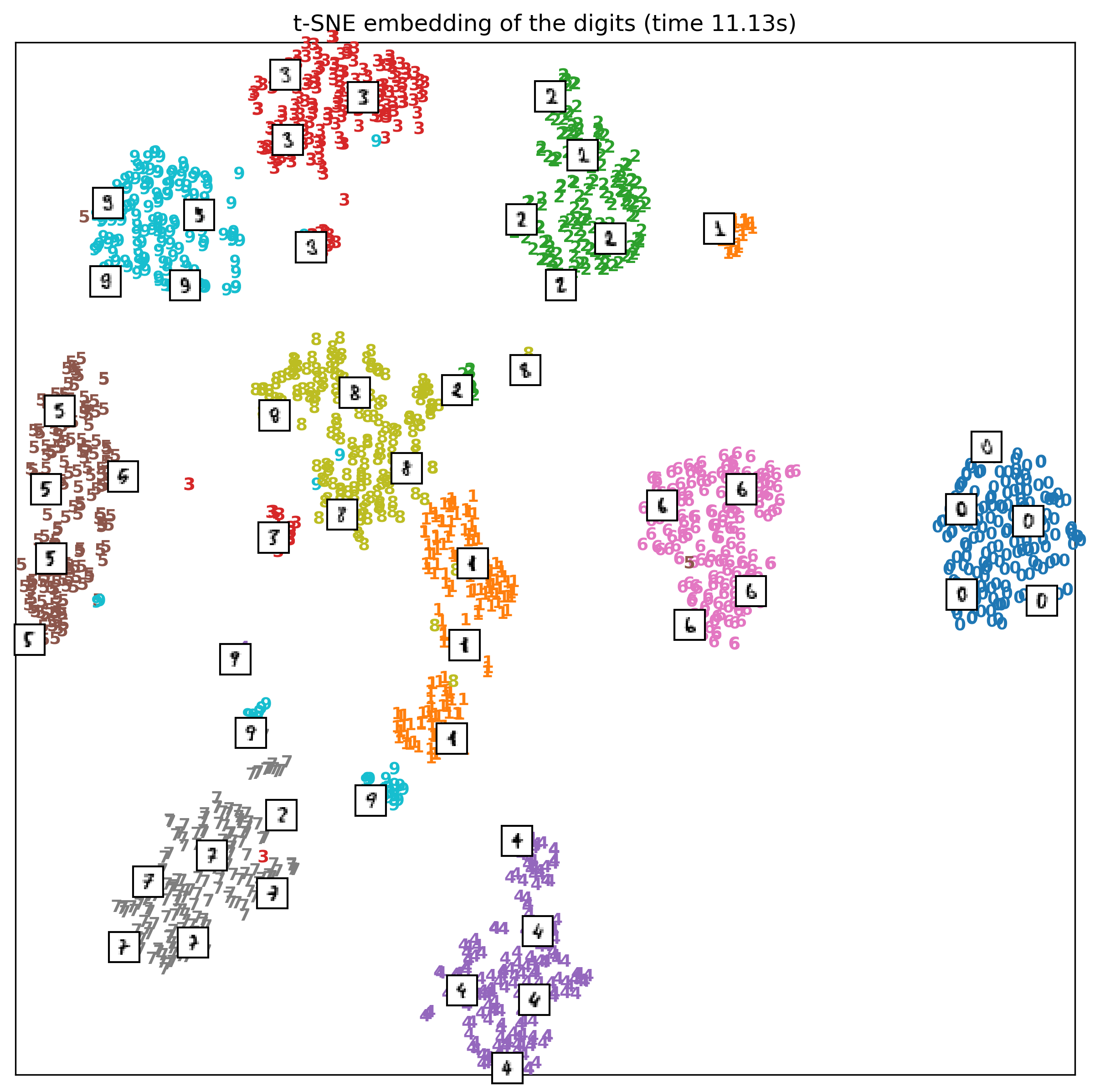
Tuning t-SNE perplexity

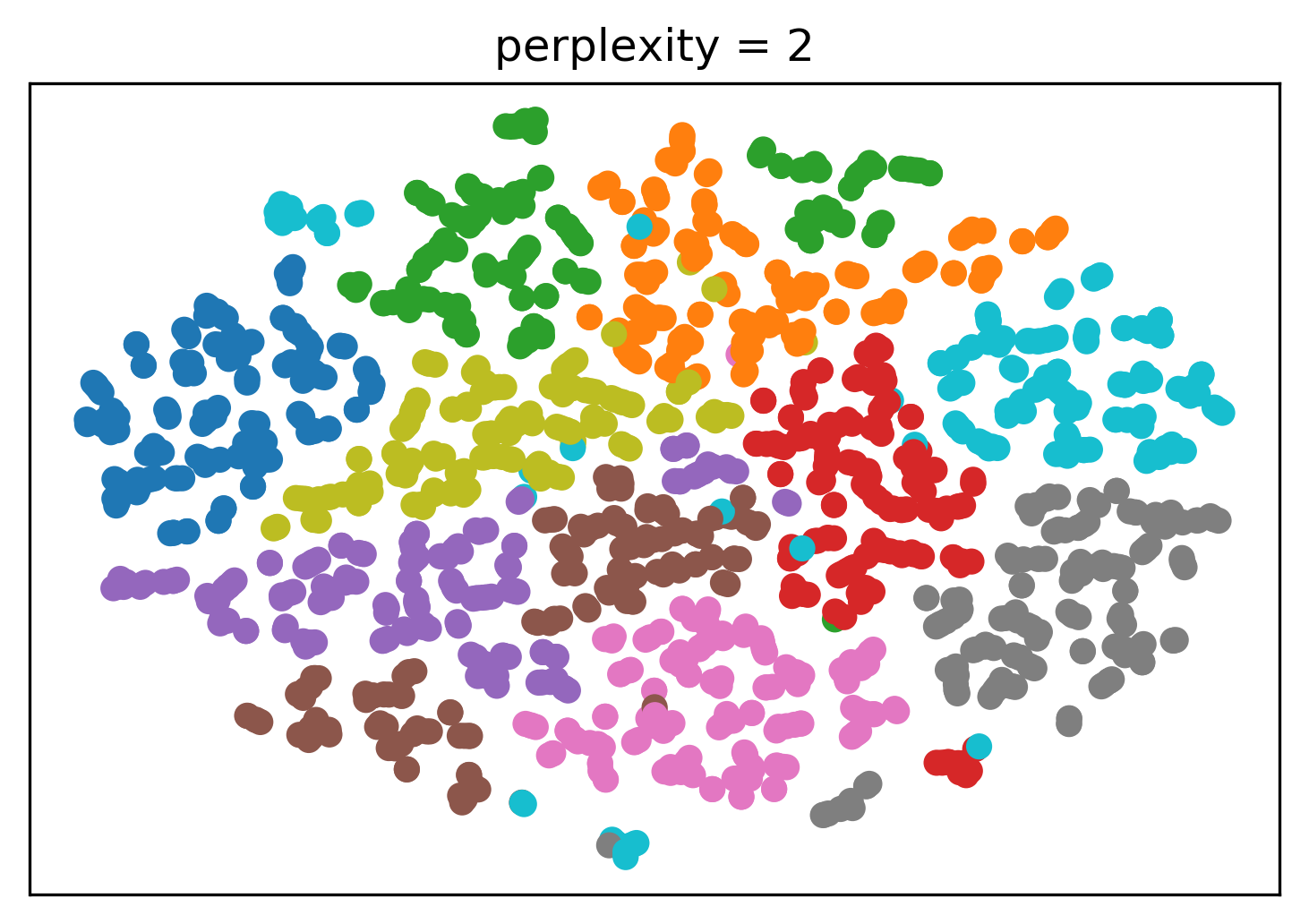
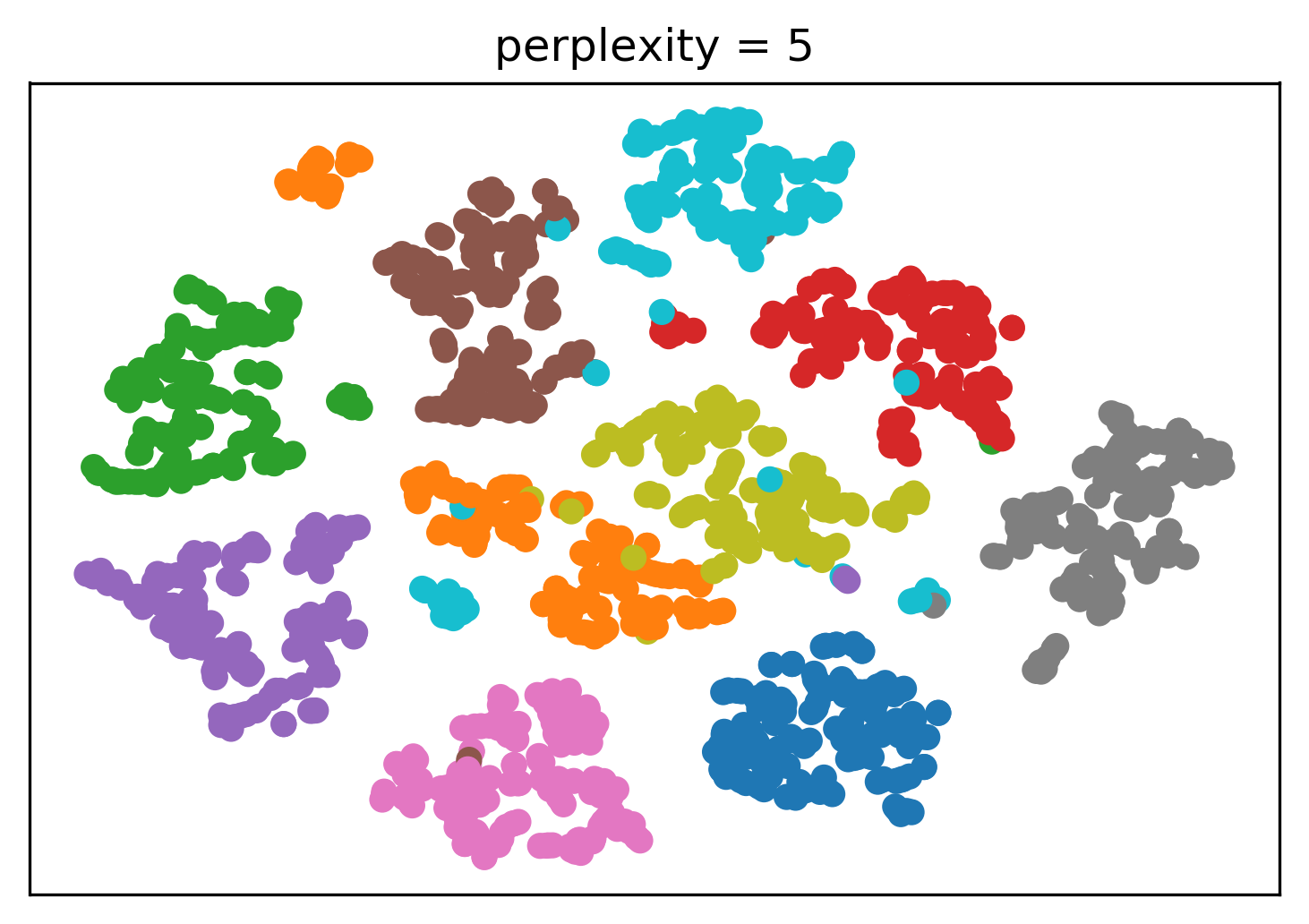
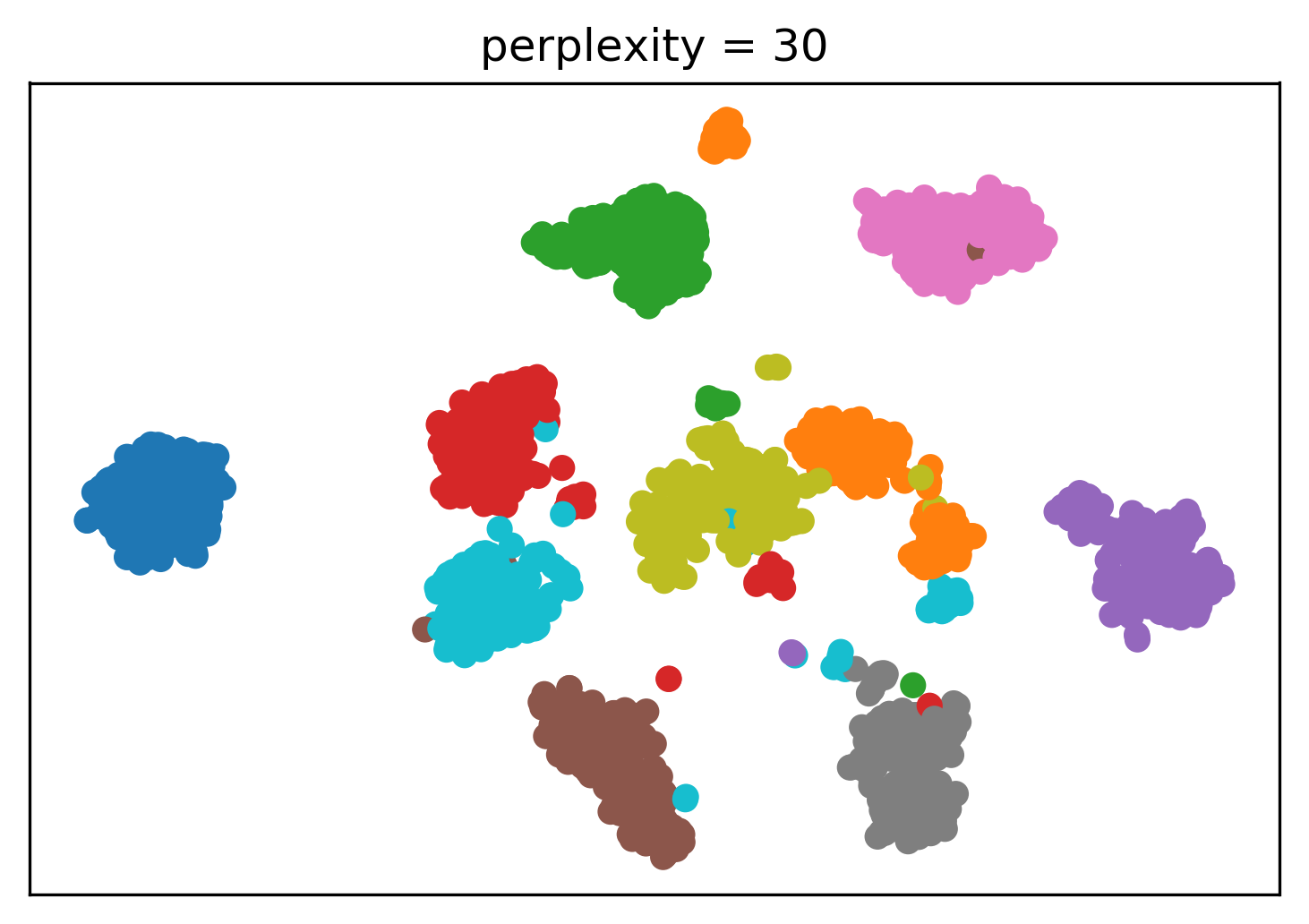
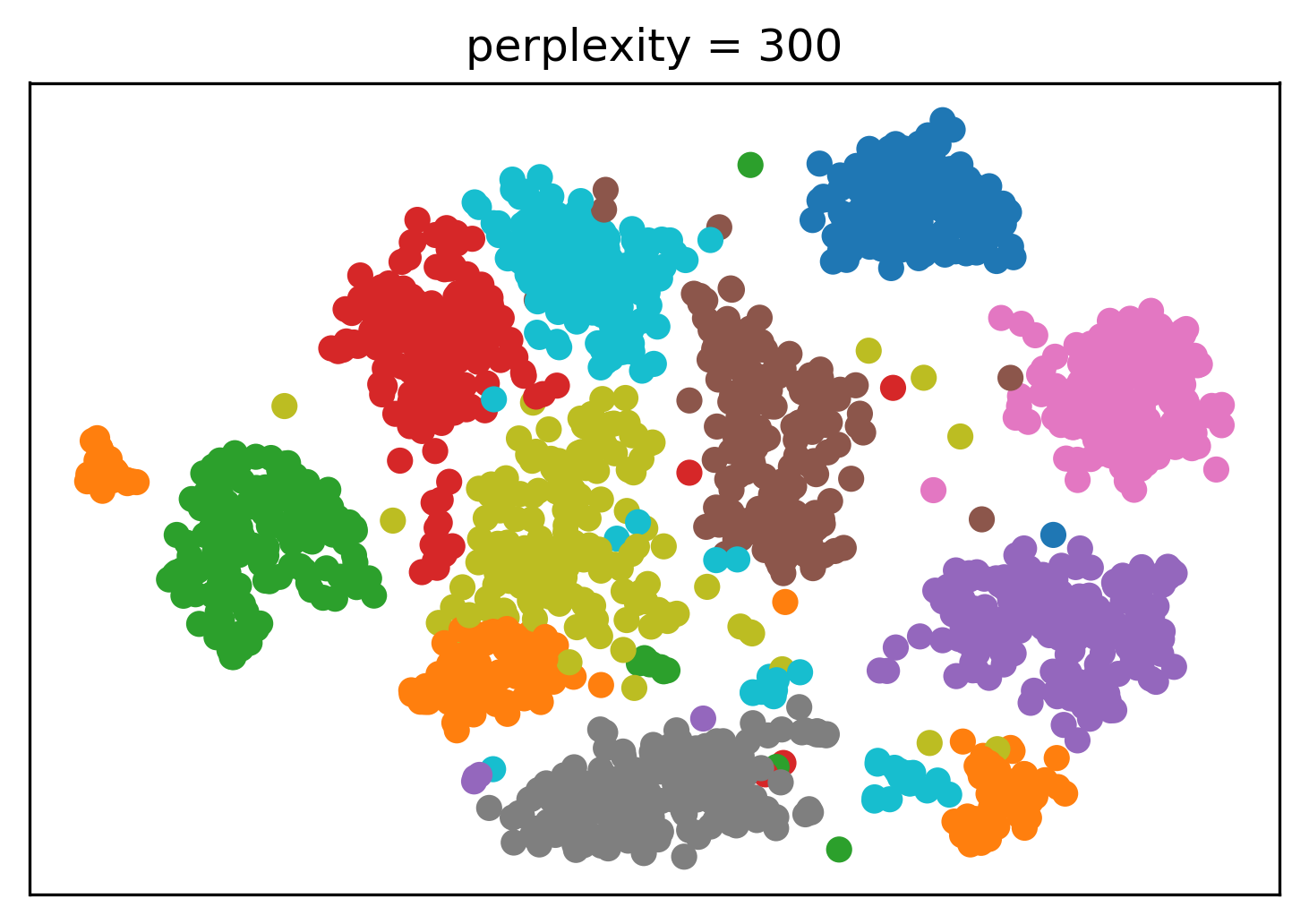
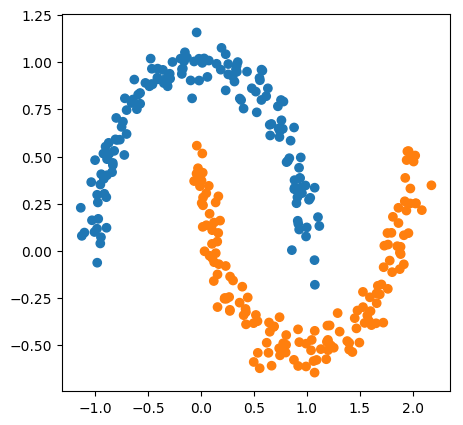
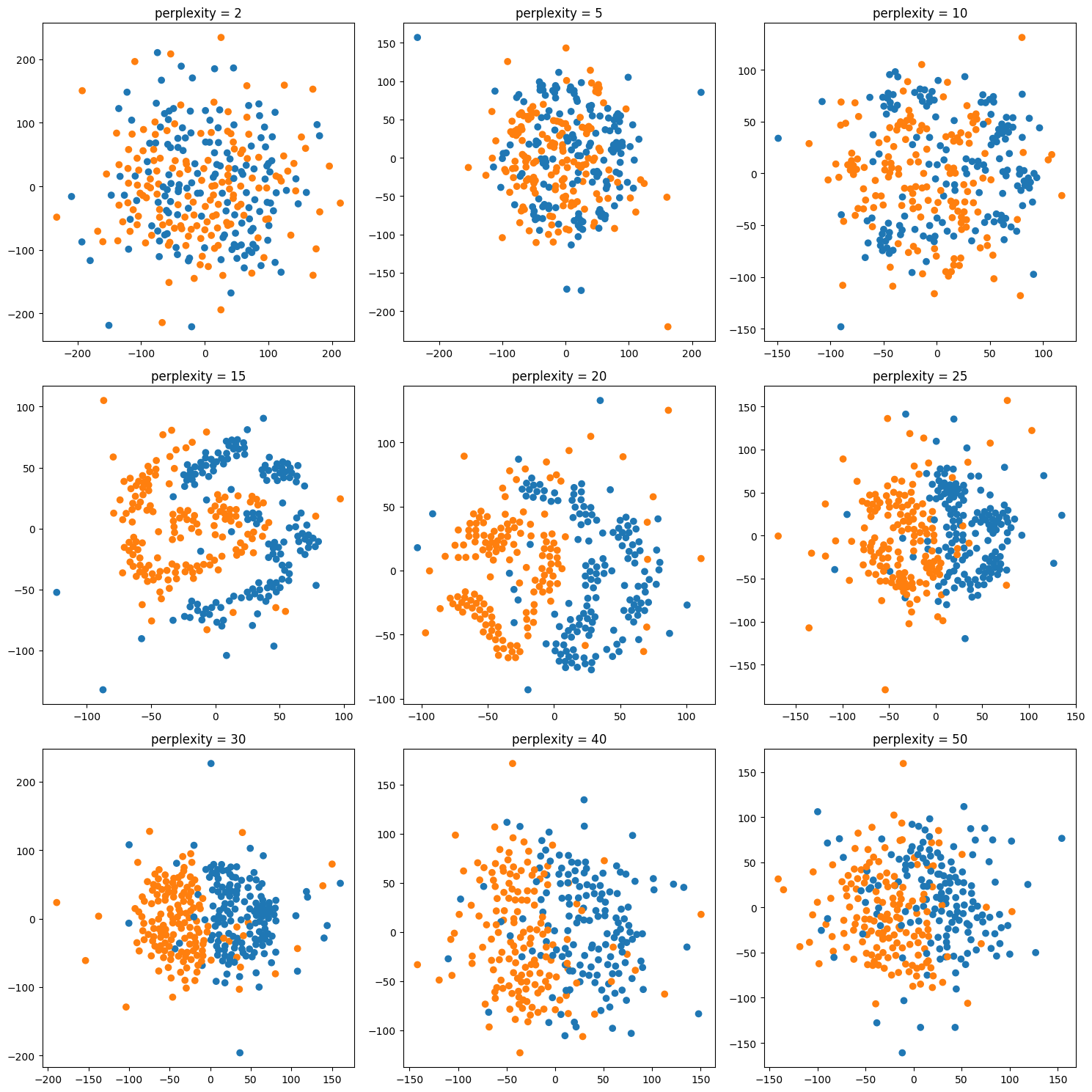
Play around online

http://distill.pub/2016/misread-tsne/

Discriminant Analysis

Linear Discriminant Analysis aka Fisher Discriminant

\[ P(y=k | X) = \frac{P(X | y=k) P(y=k)}{P(X)} = \frac{P(X | y=k) P(y = k)}{ \sum_{l} P(X | y=l) \cdot P(y=l)}\]

\[ p(X | y=k) = \frac{1}{(2\pi)^n |\Sigma|^{1/2}}\exp\left(-\frac{1}{2} (X-\mu_k)^t \Sigma^{-1} (X-\mu_k)\right) \]

\[ \log\left(\frac{P(y=k|X)}{P(y=l | X)}\right) = 0 \Leftrightarrow (\mu_k-\mu_l)\Sigma^{-1} X = \frac{1}{2} (\mu_k^t \Sigma^{-1} \mu_k - \mu_l^t \Sigma^{-1} \mu_l) \]

Quadratic Discriminant Analysis

\[ p(X | y=k) = \frac{1}{(2\pi)^n |\Sigma_k|^{1/2}}\exp\left(-\frac{1}{2} (X-\mu_k)^t \Sigma_k^{-1} (X-\mu_k)\right) \]

Comparison

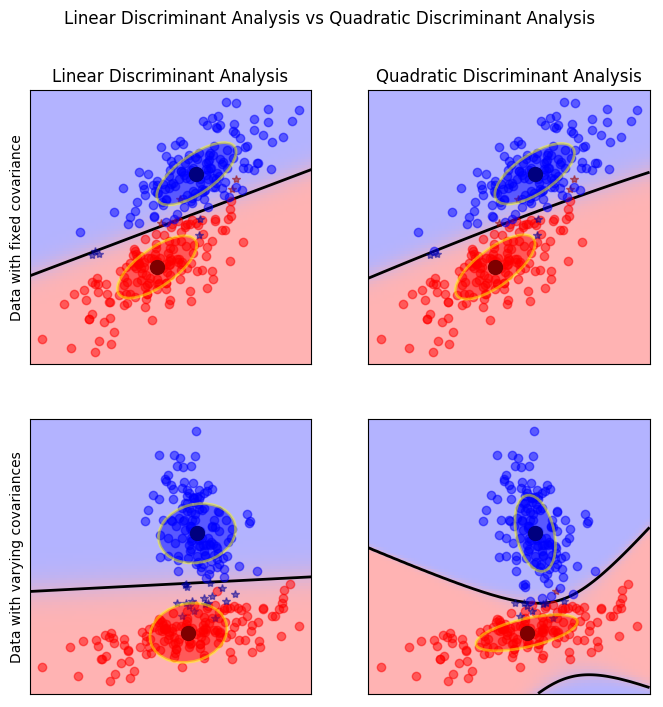
Discriminants and PCA

Both fit Gaussian model
PCA for the whole data
LDA multiple Gaussians with shared covariance
Can use LDA to transform space
At most as many components as there are classes - 1 (needs between-class variance)

PCA vs Linear Discriminants

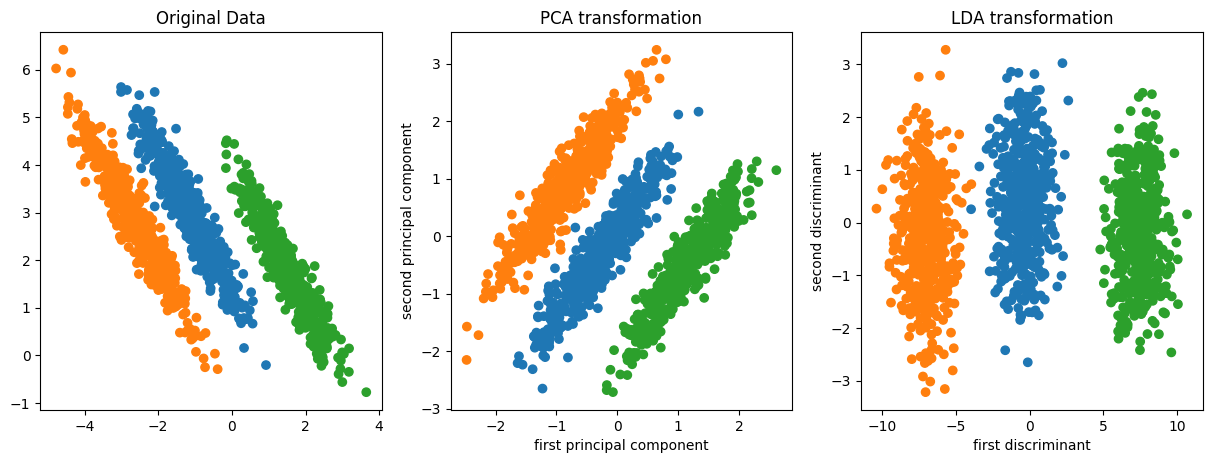
Data where PCA failed

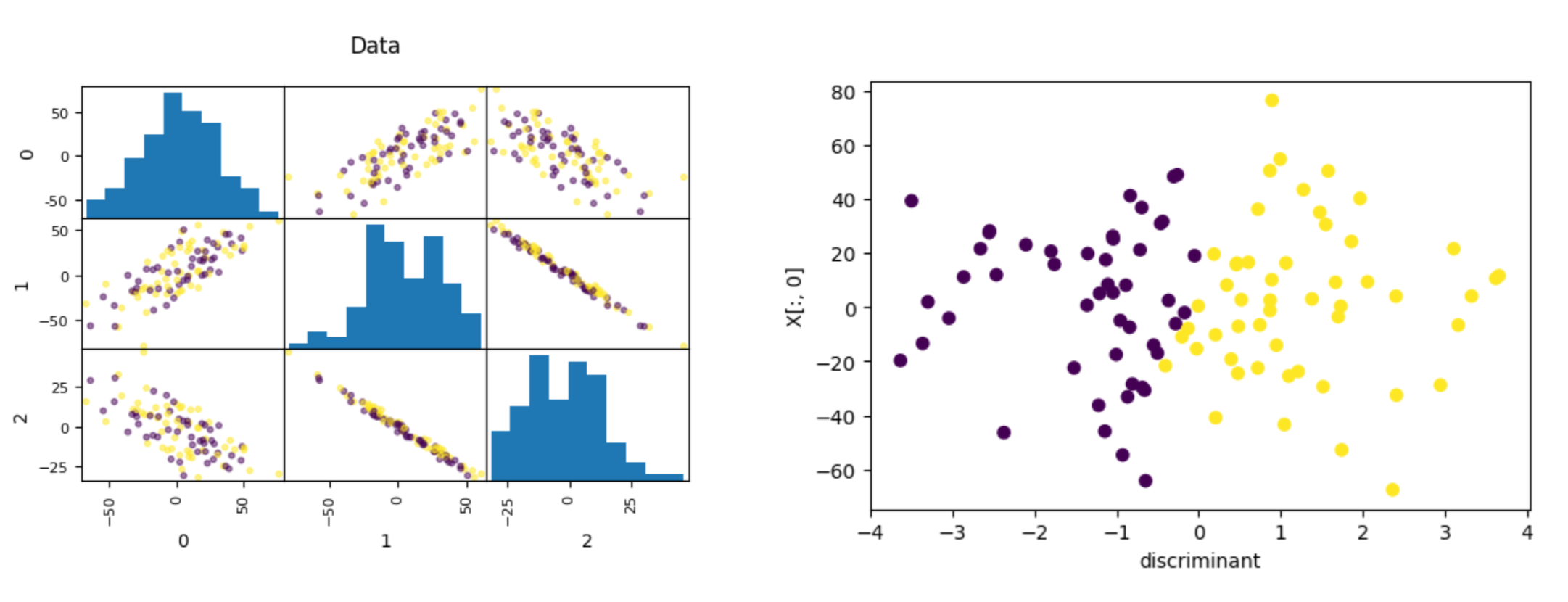
Summary

PCA good for visualization, exploring correlations
PCA can sometimes help with classification as regularization or for feature extraction
Manifold learning makes nice pictures
LDA is a supervised alternative to PCA