Decision Trees

10/17/2022

Robert Utterback (based on slides by Andreas Muller)
\( \renewcommand{\vec}[1]{\boldsymbol{#1}} \newcommand{\E}{\mathop{\boldsymbol{E}}} \newcommand{\var}{\boldsymbol{Var}} \newcommand{\norm}[1]{\lvert\lvert#1\rvert\rvert} \newcommand{\abs}[1]{\lvert#1\rvert} \newcommand{\ltwo}[1]{\norm{#1}_2} \newcommand{\lone}[1]{\norm{#1}_1} \newcommand{\sgn}[1]{\text{sign}\left( #1 \right)} \newcommand{\e}{\mathrm{e}} \newcommand{\minw}{\min_{\vec{w} \in \mathbb{R}^p, b\in\mathbb{R}}} \newcommand{\summ}{\sum_{i=1}^m} \newcommand{\sumn}{\sum_{i=1}^n} \newcommand{\logloss}{\ln{(\exp{(-y^{(i)}(\vec{w}^T\vec{x}^{(i)}+b))} + 1)}} \newcommand{\ai}{\alpha^{(i)}} \newcommand{\w}{\vec{w}} \newcommand{\wt}{\vec{w}^T} \newcommand{\xi}{\vec{x}^{(i)}} \newcommand{\xit}{(\vec{x}^{(i)})^T} \newcommand{\xip}{\xit \vec{w}} \newcommand{\tip}{(\phi(\xi)^T \phi(\vec{x}))} \)

Decision Trees

Why Trees?

  • Very powerful modeling method – non-linear!
  • Don't care about scaling or distribution of data!
  • Interpretable
  • Basis of very powerful models!

Decision Trees for Classification

Idea: series of binary questions

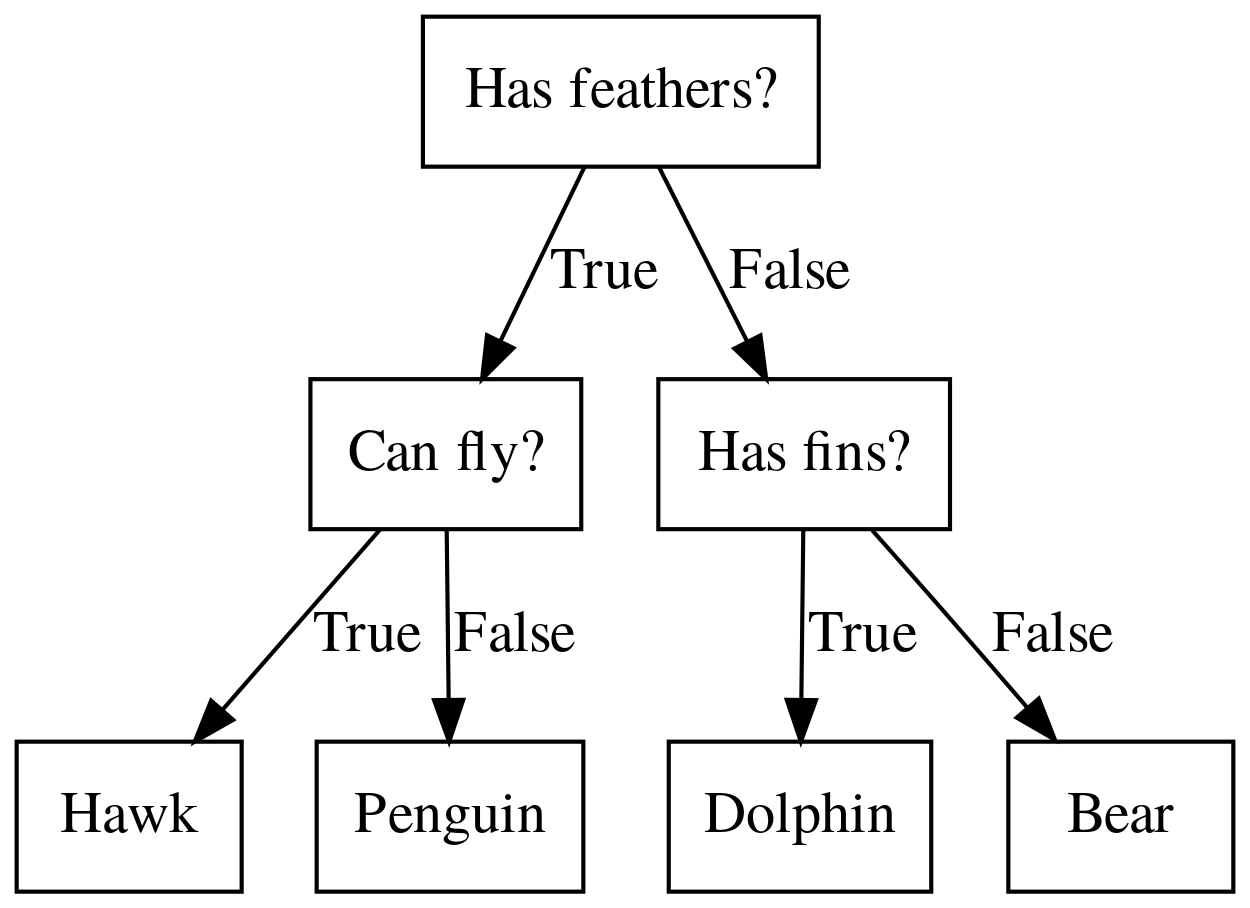
tree01.png

Building Trees (CART)

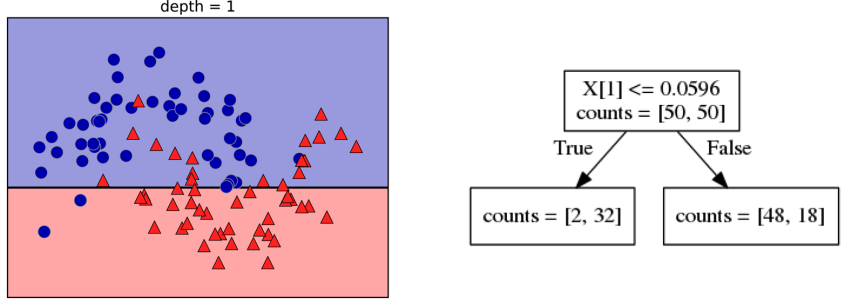
tree02.png

Continuous features:

  • “questions” are thresholds on single features.
  • Minimize impurity

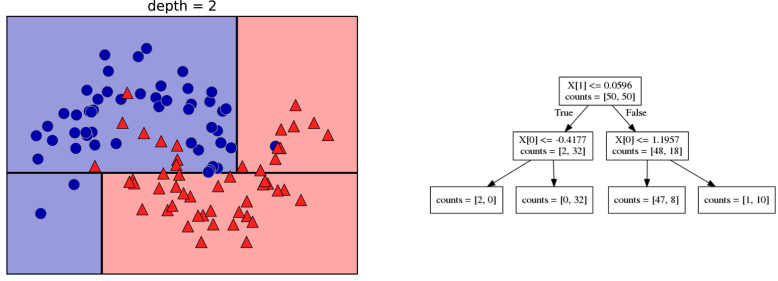
tree03.png

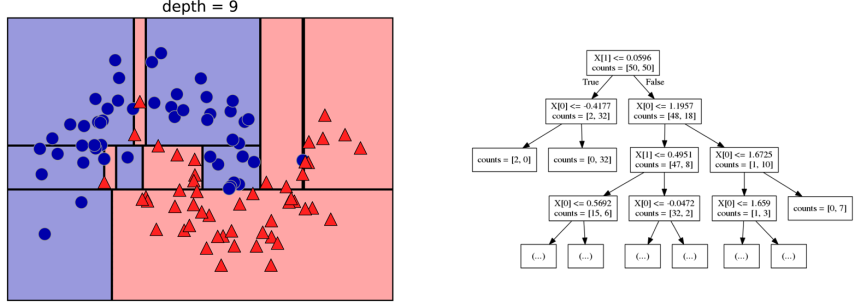
tree04.png

Criteria (for classification)

  • Gini Index: \(H_\text{gini}(X_m) = \sum_{k\in\mathcal{Y}} p_{mk} (1 - p_{mk})\)
  • Cross-Entropy: \(H_\text{CE}(X_m) = -\sum_{k\in\mathcal{Y}} p_{mk} \log(p_{mk})\)
  • \(x_m\) observations in node m
  • \(\mathcal{Y}\) classes
  • \(p_m\) distribution over classes in node m

Prediction

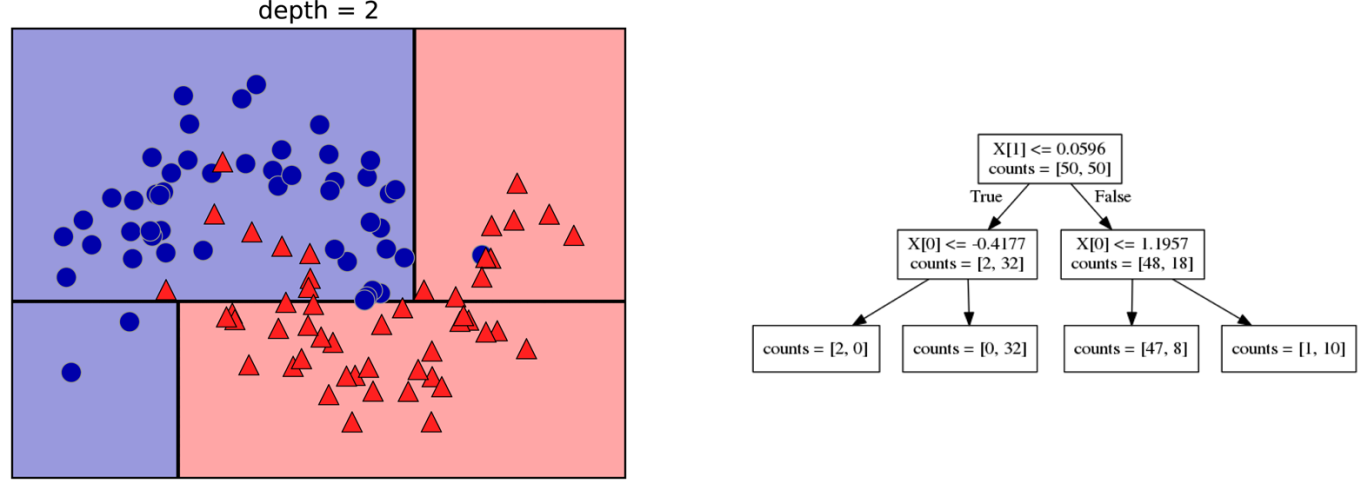
tree05.png

Regression trees

Regression Tree math

\[\text{Prediction: } \bar{y}_m = \frac{1}{N_m} \sum_{i \in N_m} y_i \]

\[ \text{Mean Squared Error: } H(X_m) = \frac{1}{N_m} \sum_{i \in N_m} (y_i - \bar{y}_m)^2 \]

\[ \text{Mean Absolute Error: } H(X_m) = \frac{1}{N_m} \sum_{i \in N_m} |y_i - \bar{y}_m| \]

Visualizing Trees

Visualizing trees with sklearn

from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = \
    train_test_split(cancer.data,cancer.target,
                     stratify=cancer.target,
                     random_state=0)
from sklearn.tree import DecisionTreeClassifier, \
    export_graphviz
tree = DecisionTreeClassifier(max_depth=2)
tree.fit(X_train, y_train) 
# tree visualization (or sklearn.tree.plot_tree)
tree_dot = export_graphviz(tree, out_file=None,
                           feature_names=cancer.feature_names)
print(tree_dot)

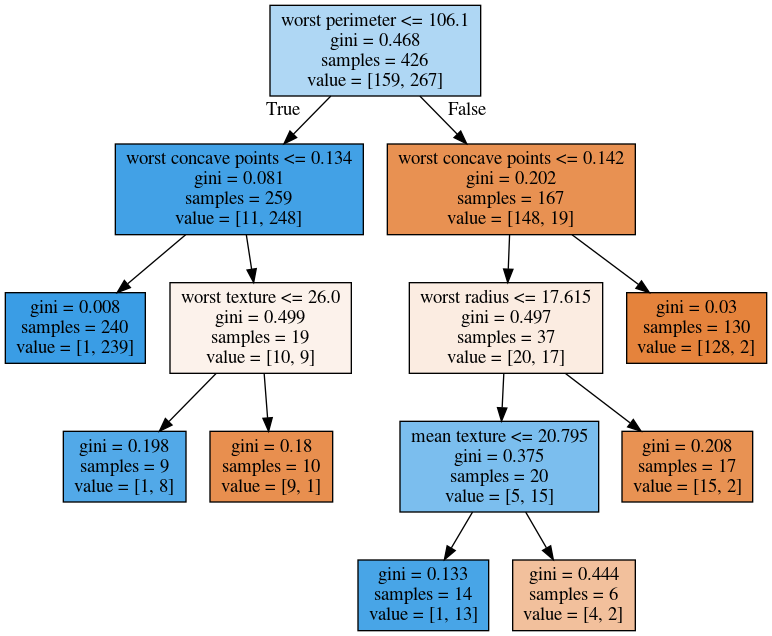
Visualizing trees with sklearn

digraph Tree {
node [shape=box, fontname="helvetica"] ;
edge [fontname="helvetica"] ;
0 [label="worst perimeter <= 106.1\ngini = 0.468\nsamples = 426\nvalue = [159, 267]"] ;
1 [label="worst concave points <= 0.134\ngini = 0.081\nsamples = 259\nvalue = [11, 248]"] ;
0 -> 1 [labeldistance=2.5, labelangle=45, headlabel="True"] ;
2 [label="gini = 0.008\nsamples = 240\nvalue = [1, 239]"] ;
1 -> 2 ;
3 [label="gini = 0.499\nsamples = 19\nvalue = [10, 9]"] ;
1 -> 3 ;
4 [label="worst concave points <= 0.142\ngini = 0.202\nsamples = 167\nvalue = [148, 19]"] ;
0 -> 4 [labeldistance=2.5, labelangle=-45, headlabel="False"] ;
5 [label="gini = 0.497\nsamples = 37\nvalue = [20, 17]"] ;
4 -> 5 ;
6 [label="gini = 0.03\nsamples = 130\nvalue = [128, 2]"] ;
4 -> 6 ;
}

Showing dot files in Jupyter

Requires graphviz C library and Python library 

!pip install graphviz

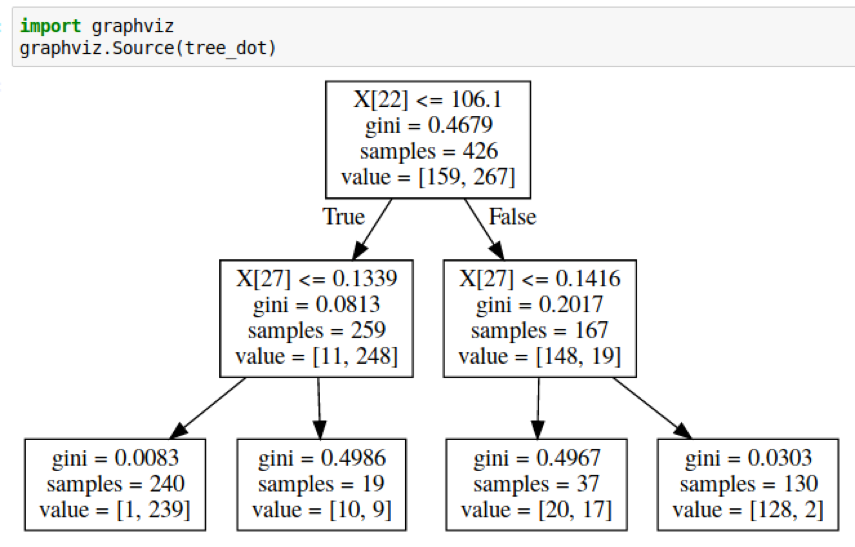
tree06.png

Producing Images from Command Line

  dot -Tpng cancer_tree.dot -o cancer_tree.png

Visualizing Trees Directly with sklearn

  from sklearn.tree import plot_tree
  tree_dot = plot_tree(tree, feature_names=cancer.feature_names)

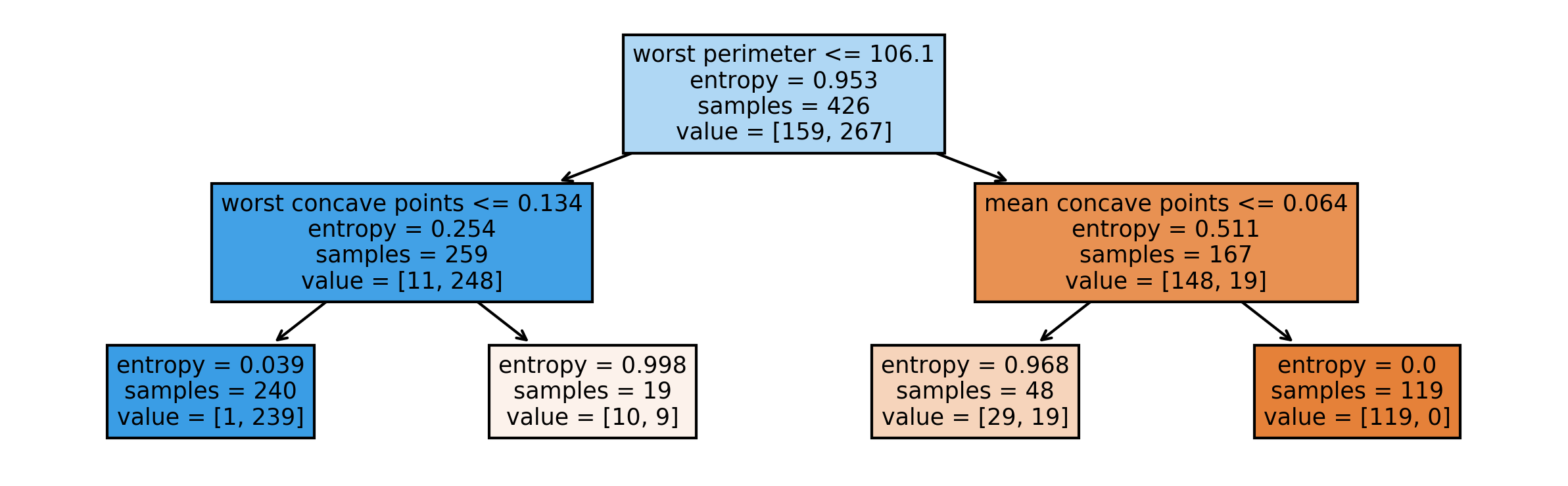
mpl_tree_plot.png

Parameter Tuning

Parameters

  • Pre-pruning and post-pruning
  • Limit tree size (pick one, maybe two):
  • max_depth
  • max_leaf_nodes
  • min_samples_split
  • min_impurity_decrease

No pruning

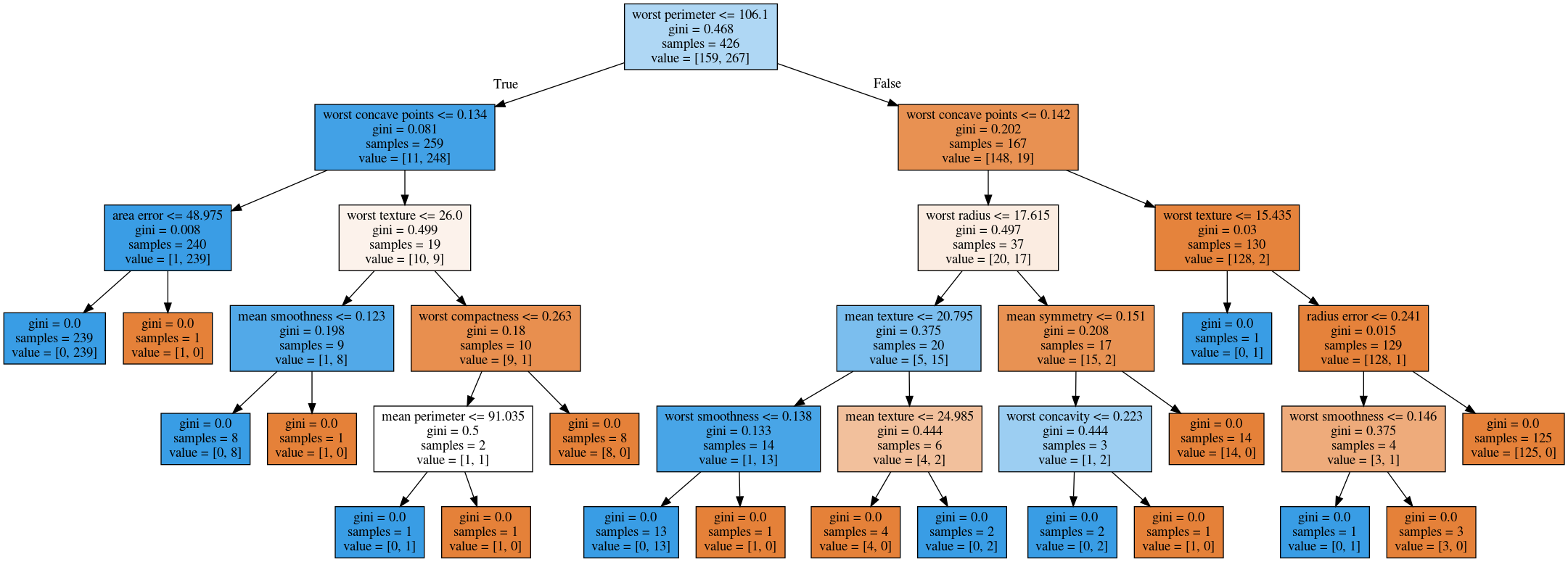
no_pruning.png

max_depth = 4

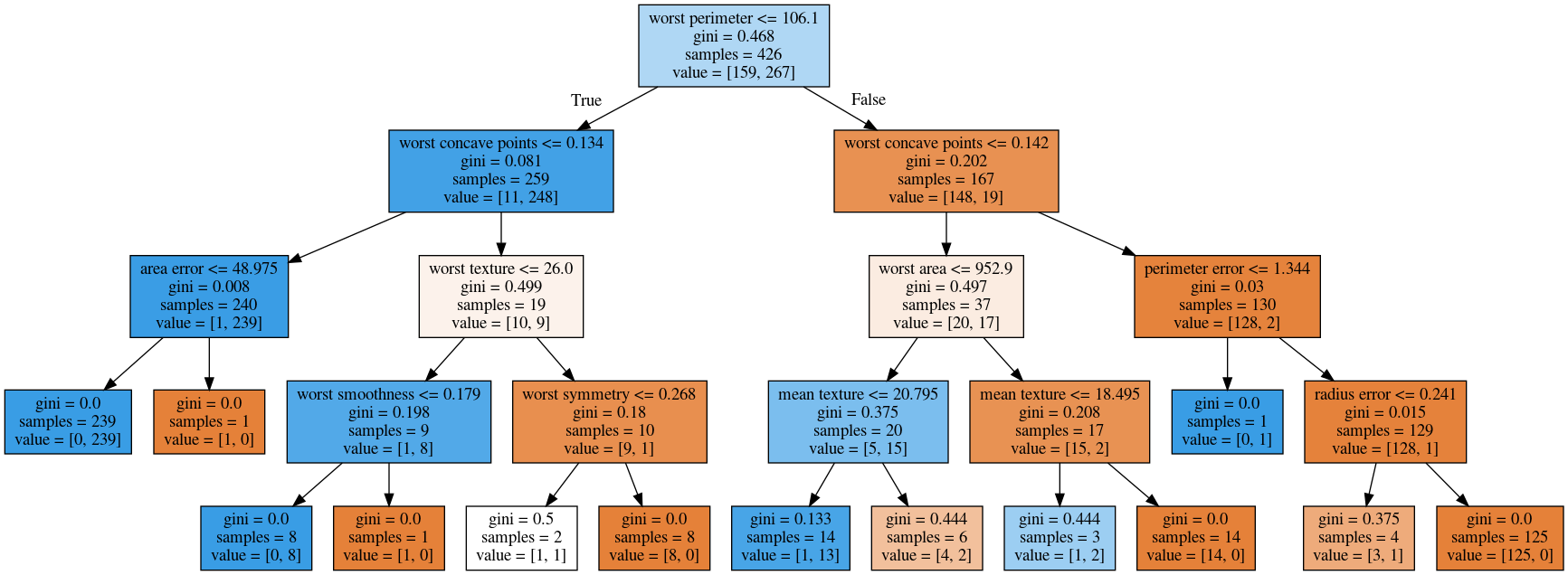
max_depth_4.png

max_leaf_nodes = 8

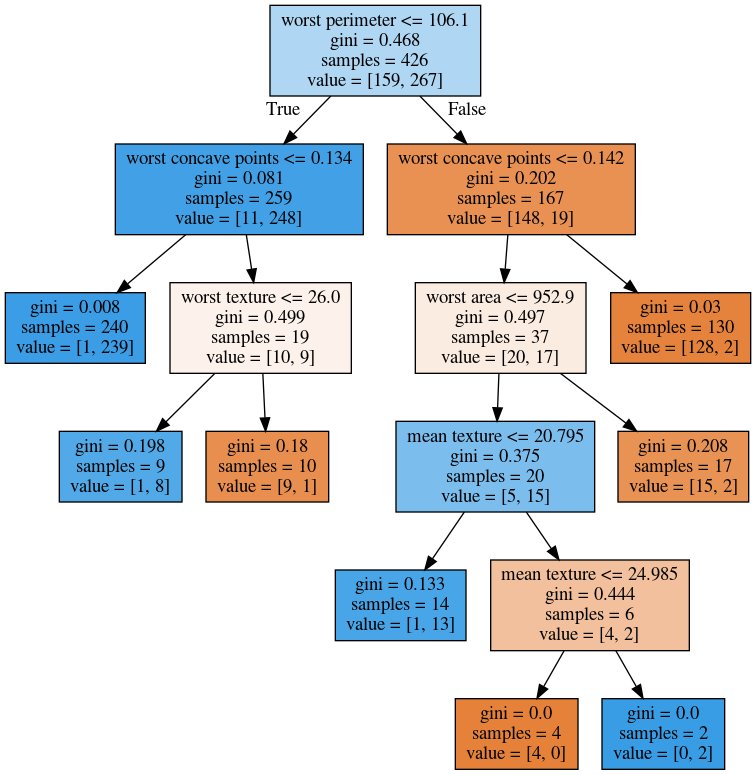
max_leaf_nodes_8.png

min_samples_split = 50

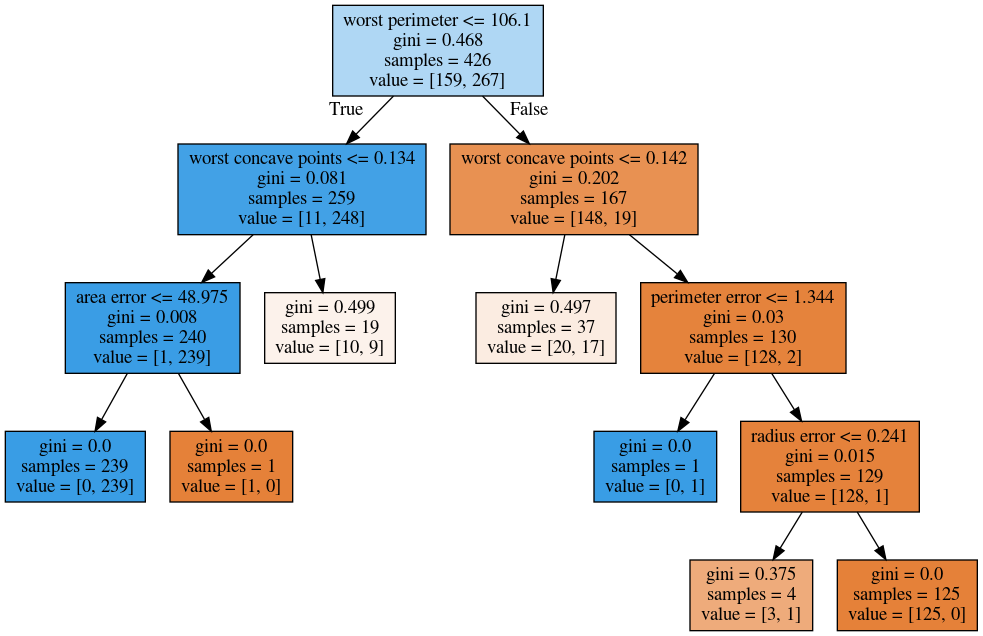
min_samples_split_50.png 

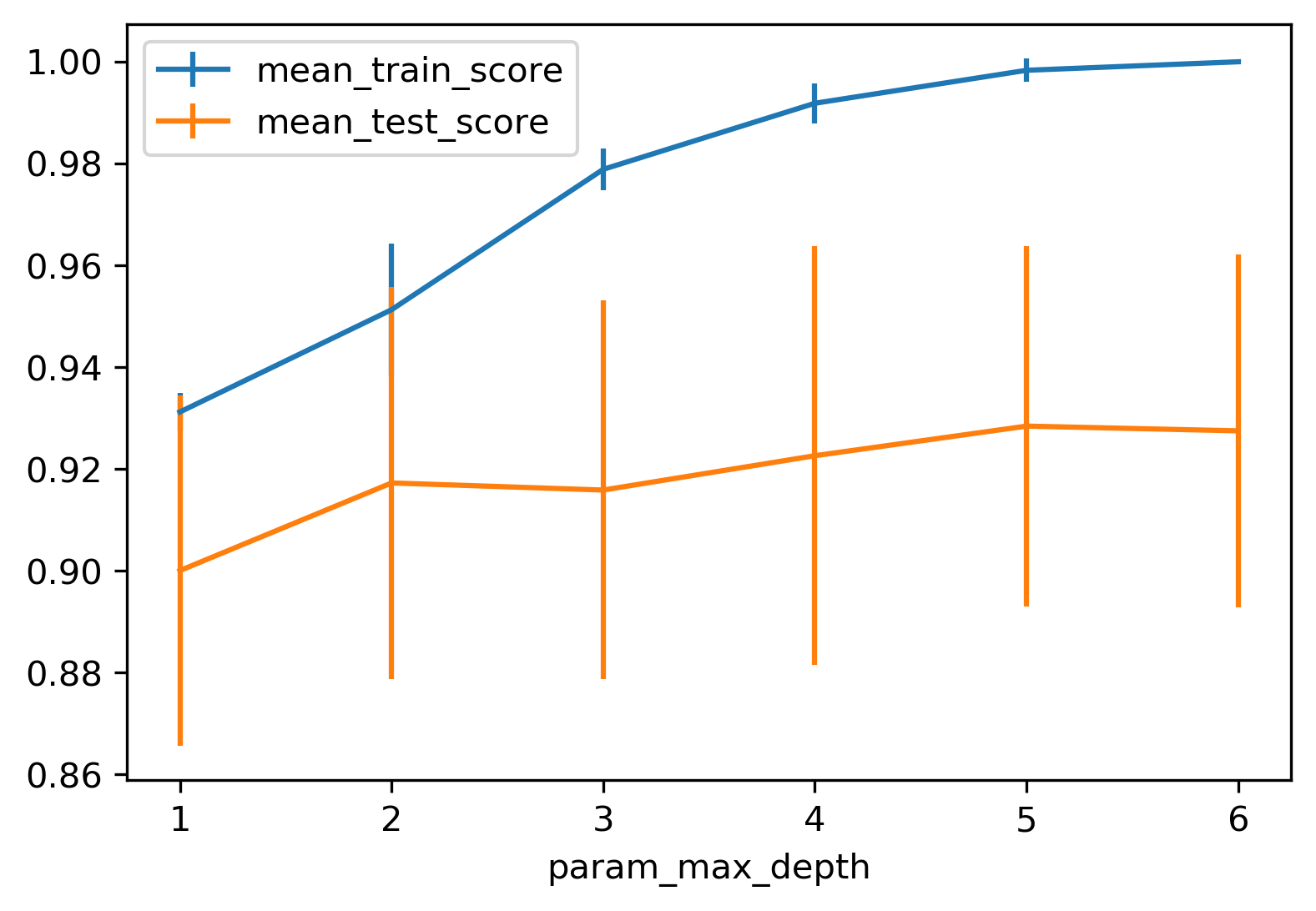
from sklearn.model_selection import GridSearchCV
param_grid = {'max_depth':range(1, 7)}
grid = GridSearchCV(DecisionTreeClassifier(random_state=0),
                    param_grid=param_grid,
                    cv=10)
grid.fit(X_train, y_train)

grid_max_depth.png 

from sklearn.model_selection import GridSearchCV
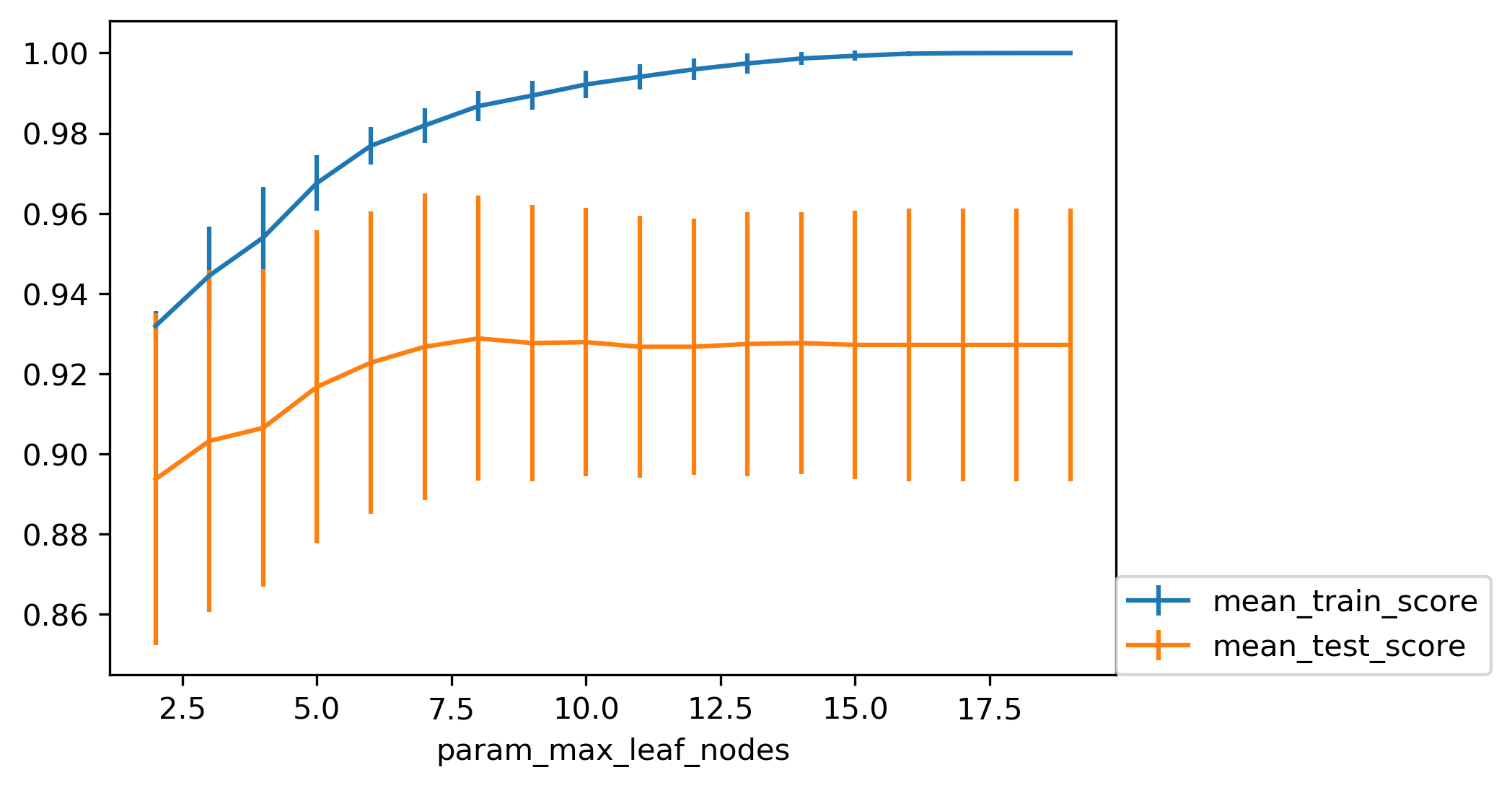
param_grid = {'max_leaf_nodes':range(2, 20)}
grid = GridSearchCV(DecisionTreeClassifier(random_state=0),
                    param_grid=param_grid, cv=10)
grid.fit(X_train, y_train)

grid_max_leaf_nodes.png

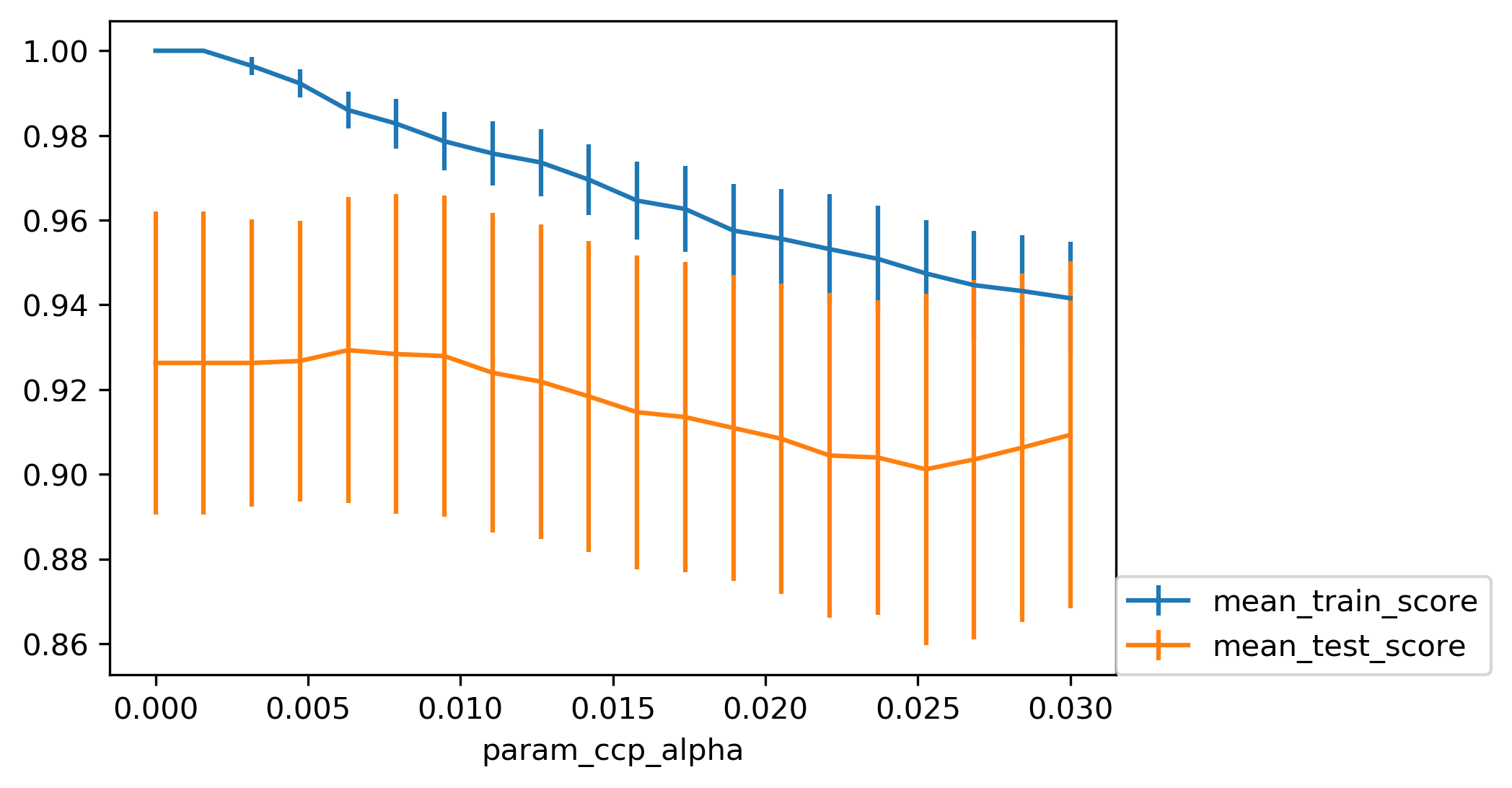
Cost Complexity (Post-) Pruning

\[ R_\alpha(T) = R(T) + \alpha |T| \]

  • \(R(T)\) is total leaf impurity
  • \(|T|\) is number of leaf nodes
  • \(\alpha\) is hyperparameter

  param_grid = {'ccp_alpha': np.linspace(0.0, 0.03, 20)}
  grid = GridSearchCV(DecisionTreeClassifier(random_state=0),
		      param_grid=param_grid, cv=10)
  grid.fit(X_train, y_train)

grid_ccp_alpha.png

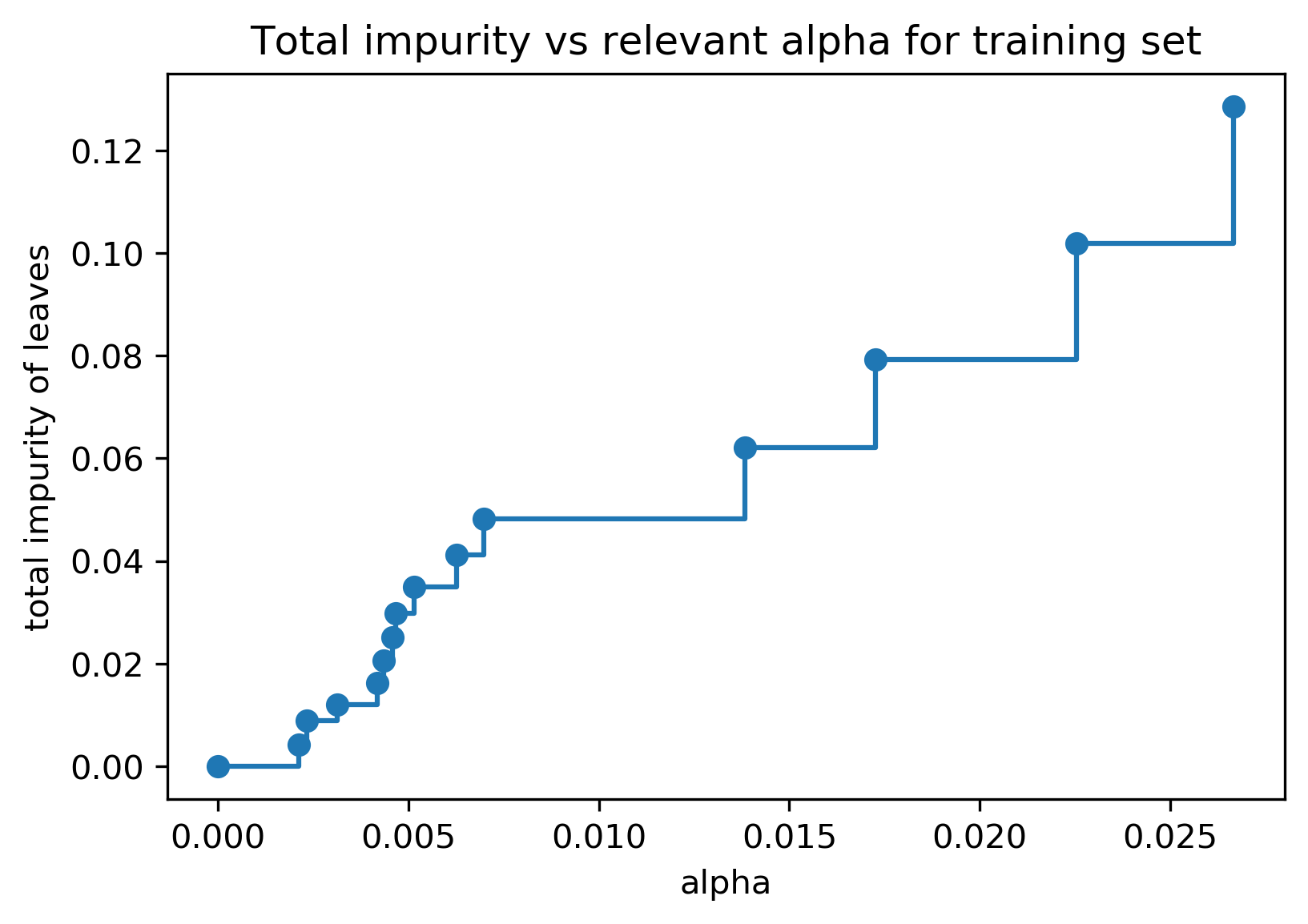
Efficient Pruning

  clf = DecisionTreeClassifier(random_state=0)
  path = clf.cost_complexity_pruning_path(X_train, y_train)
  ccp_alphas, impurities = path.ccp_alphas, path.impurities

pruning_alpha.png

Post-pruned vs. Pre-pruned

Cost-complexity pruning

tree_pruned.png

Max leaf nodes search

max_leaf_nodes_8.png

Weaknesses

RAM Price over Time

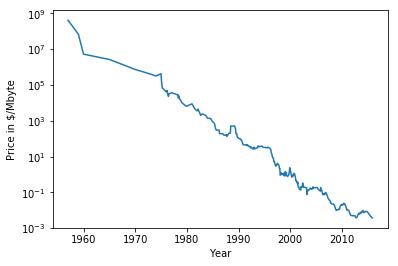
treeextrap01.png

Extrapolation

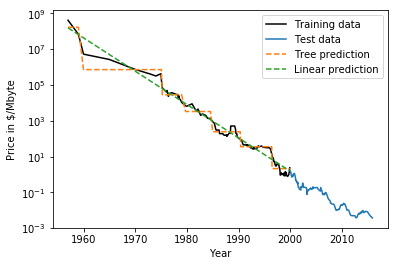
treeextrap02.png

Extrapolation

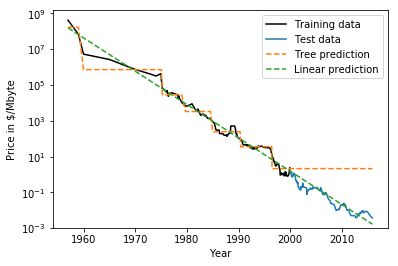
treeextrap03.png

Relation to Nearest Neighbors

  • Predict average of neighbors – either by k, by epsilon ball or by leaf.
  • Trees are much faster to predict.
  • Neither can extrapolate

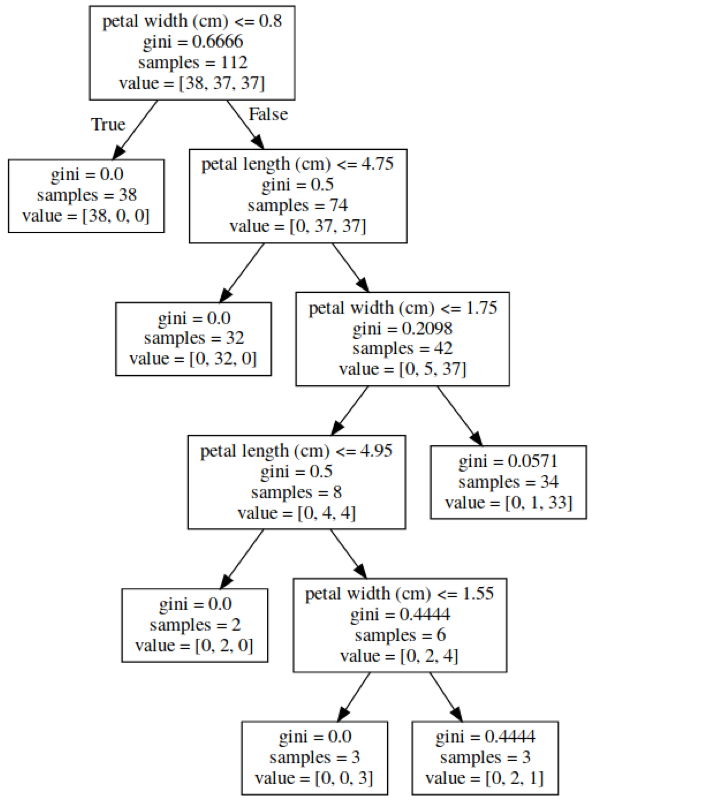
Instability

X_train, X_test, y_train, y_test = \
    train_test_split(iris.data,
                     iris.target,
                     stratify=iris.target,
                     random_state=0)
tree = DecisionTreeClassifier(max_leaf_nodes=6)
tree.fit(X_train, y_train)

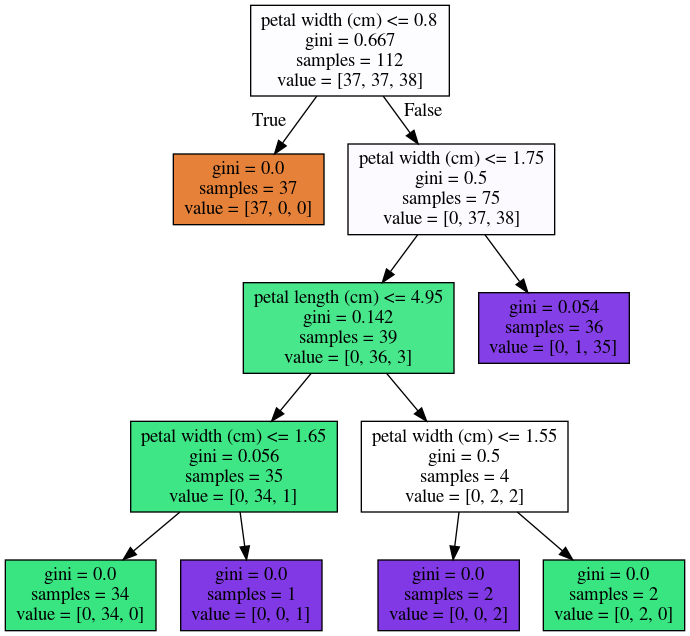
instability_1.png 

X_train, X_test, y_train, y_test = \
    train_test_split(iris.data,
                     iris.target,
                     stratify=iris.target,
                     random_state=1)
tree = DecisionTreeClassifier(max_leaf_nodes=6)
tree.fit(X_train, y_train)

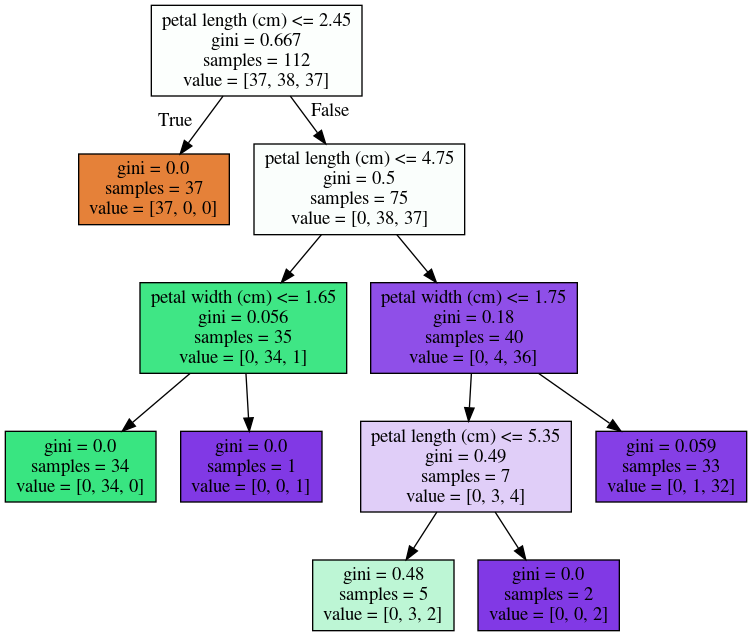
instability_2.png

Other Tree Details

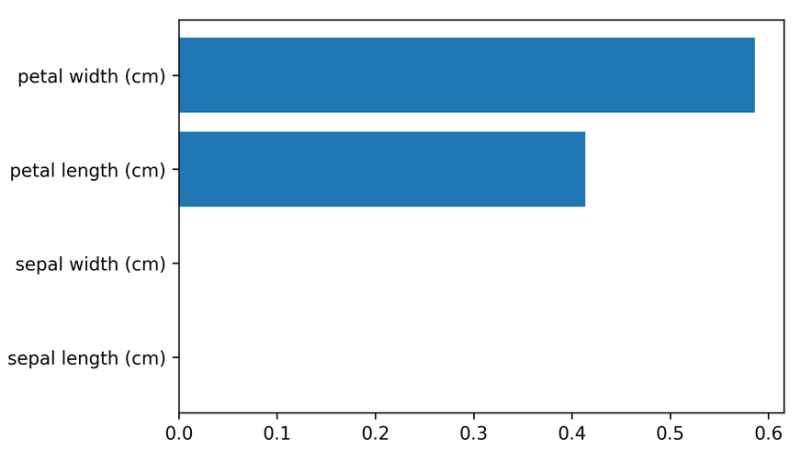
Feature importance

X_train, X_test, y_train, y_test = \
    train_test_split(iris.data,
                     iris.target,
                     stratify=iris.target,
                     random_state=1)
tree = DecisionTreeClassifier(max_leaf_nodes=6)
tree.fit(X_train,y_train)

tree13.png 

tree.feature_importances_
# array([0.0, 0.0, 0.414, 0.586])

treeimportances.png

Categorical Data

  • Can split on categorical data directly (in theory)
  • Intuitive way to split: split in two subsets
  • \(2 ^ \text{n_values}\) many possibilities
  • Possible to do in almost linear time exactly for gini index and binary classification.
  • Heuristics done in practice for multi-class.
  • Not in sklearn yet :(

Predicting probabilities

  • Fraction of class in leaf.
  • Without pruning: Always 100% certain!
  • Even with pruning might be too certain.

Conditional Inference Trees

  • Select "best" split with correcting for multiple-hypothesis testing.
  • More "fair" to categorical variables.
  • Only in R so far (party)

Different splitting methods

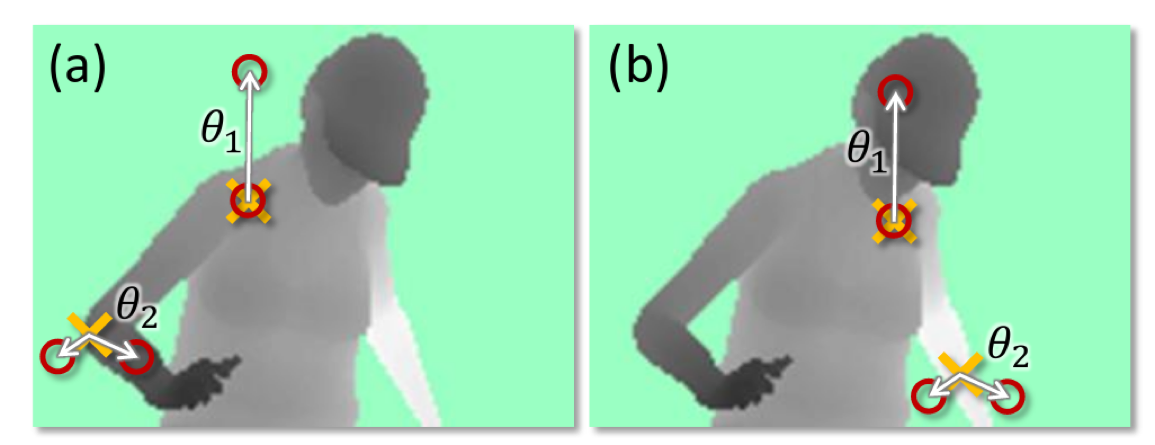pose.png (taken from Shotton et. al. Real-Time Human Pose Recognition)