SVM Kernels

10/07/2022

Robert Utterback (based on slides by Andreas Muller)
\( \renewcommand{\vec}[1]{\boldsymbol{#1}} \newcommand{\E}{\mathop{\boldsymbol{E}}} \newcommand{\var}{\boldsymbol{Var}} \newcommand{\norm}[1]{\lvert\lvert#1\rvert\rvert} \newcommand{\abs}[1]{\lvert#1\rvert} \newcommand{\ltwo}[1]{\norm{#1}_2} \newcommand{\lone}[1]{\norm{#1}_1} \newcommand{\sgn}[1]{\text{sign}\left( #1 \right)} \newcommand{\e}{\mathrm{e}} \newcommand{\minw}{\min_{\vec{w} \in \mathbb{R}^p, b\in\mathbb{R}}} \newcommand{\summ}{\sum_{i=1}^m} \newcommand{\sumn}{\sum_{i=1}^n} \newcommand{\logloss}{\ln{(\exp{(-y^{(i)}(\vec{w}^T\vec{x}^{(i)}+b))} + 1)}} \newcommand{\ai}{\alpha^{(i)}} \newcommand{\w}{\vec{w}} \newcommand{\wt}{\vec{w}^T} \newcommand{\xi}{\vec{x}^{(i)}} \newcommand{\xit}{(\vec{x}^{(i)})^T} \newcommand{\xip}{\xit \vec{w}} \newcommand{\tip}{(\phi(\xi)^T \phi(\vec{x}))} \)

Nonlinear SVMs

Motivation

  • Go from linear models to more powerful nonlinear ones.
  • Keep convexity (ease of optimization).
  • Generalize the concept of feature engineering.

Reminder on Linear SVM

\[ \minw C \sum_{i=1}^m \max(0, 1 - y^{(i)} (\vec{w}^T\vec{x}^{(i)} + b)) + ||w||^2_2 \] \[ \hat{y} = \text{sign}(\vec{w}^T \vec{x} + b) \]

Max-Margin and Support Vectors

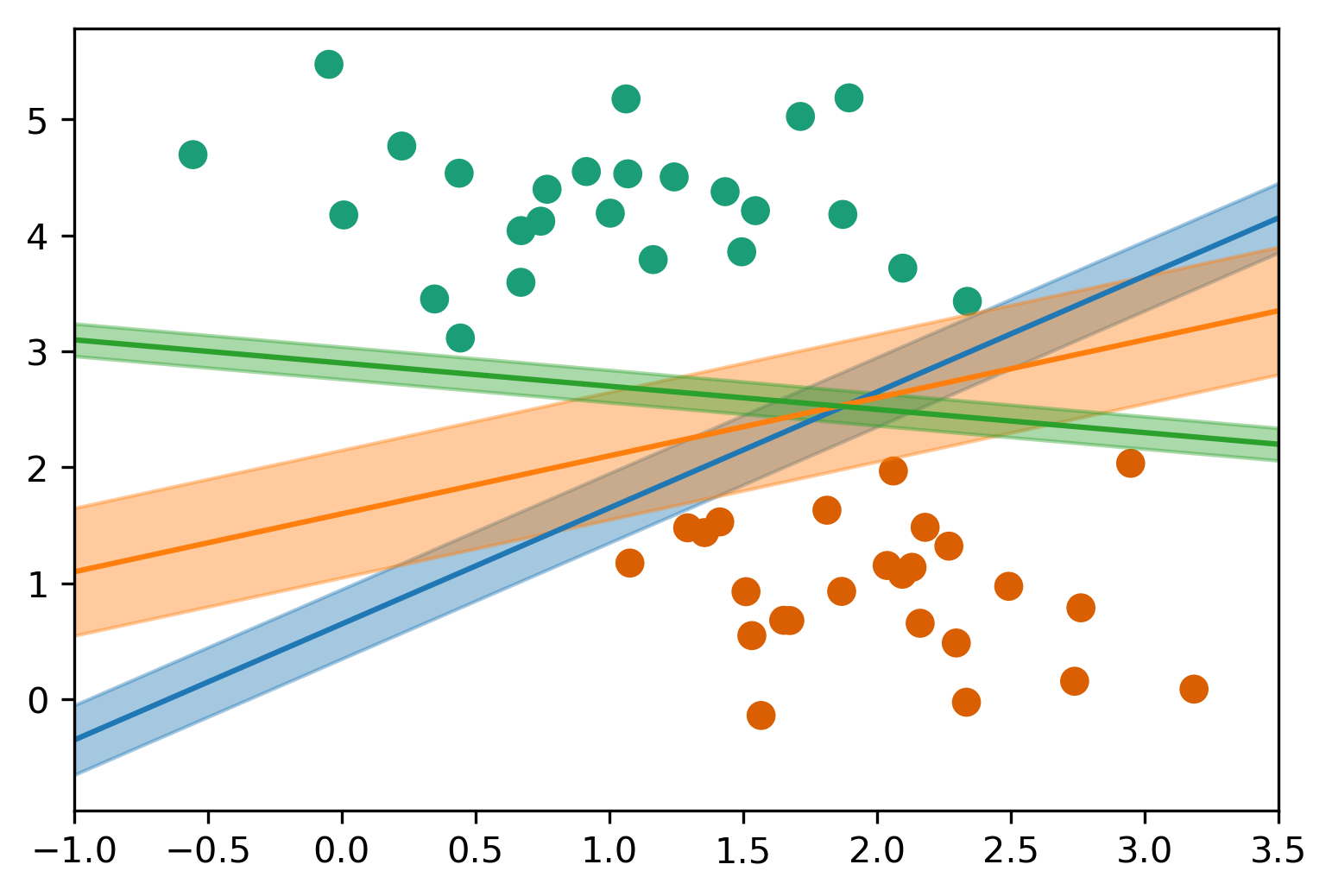
max_margin.png

Max-Margin and Support Vectors

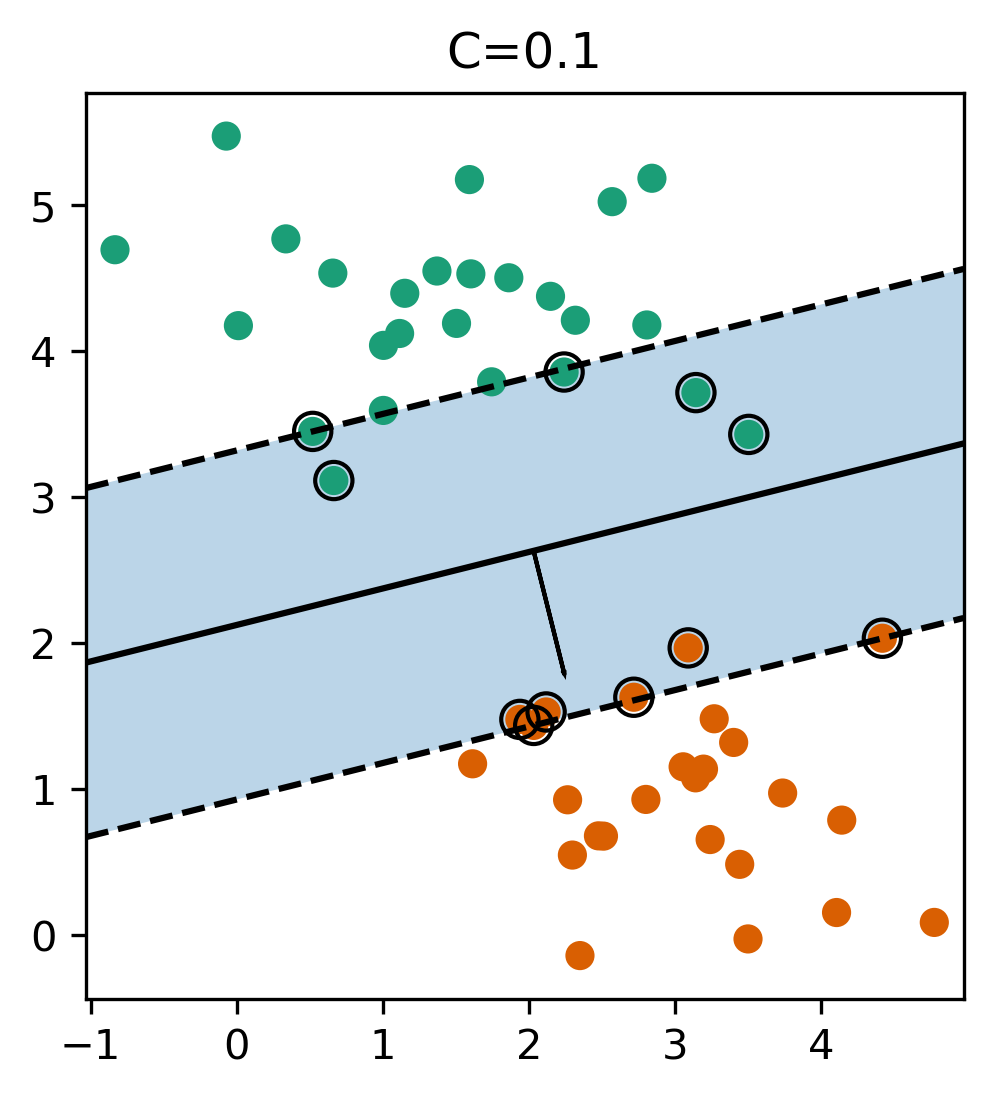
max_margin_C_0.1.png

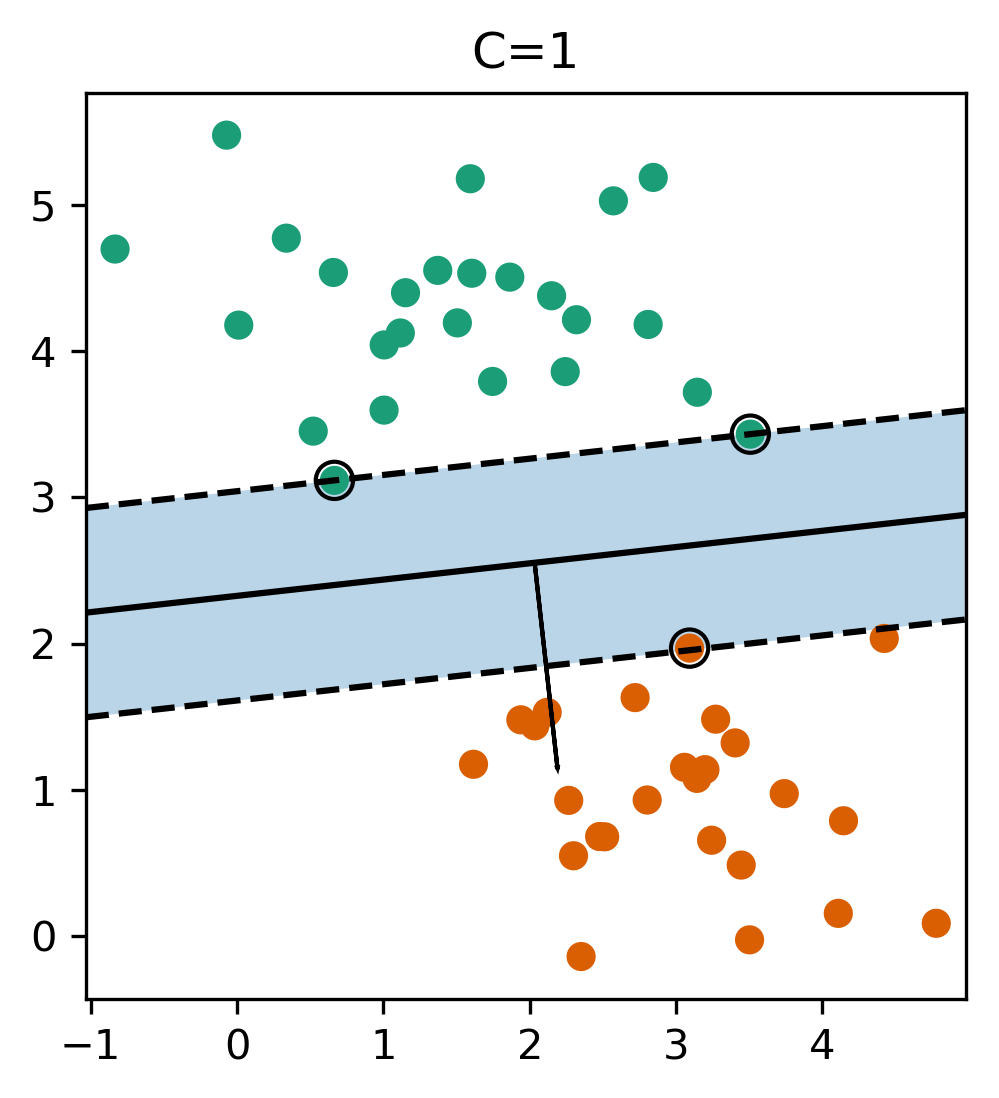
max_margin_C_1.png

Reformulate Linear Models

  • Optimization Theory:

\[ \vec{w} = \sum_{i=1}^m \alpha^{(i)} \vec{x}^{(i)} \]

(alpha are dual coefficients. Non-zero for support vectors only)

\[ \hat{y} = \text{sign}(\vec{w}^T \vec{x}) \Longrightarrow \hat{y} = \text{sign}\left(\summ\ai (\xip) \right) \]

\[ \ai \le C\]

Kernels

Introducing Kernels

\[\hat{y} = \text{sign}\left(\summ\ai (\xip)\right) \longrightarrow \\ \hat{y} = \text{sign}\left(\summ \ai \tip \right) \]

\[ \phi(\vec{x}^{(i)})^T \phi( \vec{x}^{(j)}) \longrightarrow k(\xi, \vec{x}^{(j)}) \]

Examples of Kernels

\[k_\text{linear}(\vec{x}, \vec{x}') = \vec{x}^T\vec{x}'\] \[k_\text{poly}(\vec{x}, \vec{x}') = (\vec{x}^T\vec{x}' + c) ^ d\] \[k_\text{rbf}(\vec{x}, \vec{x}') = \exp(\gamma||\vec{x} -\vec{x}'||^2)\] \[k_\text{sigmoid}(\vec{x}, \vec{x}') = \tanh\left(\gamma \vec{x}^T\vec{x}' + r\right)\] \[k_\cap(\vec{x}, \vec{x}')= \sum_{i=1}^p \min(x_i, x'_i)\]

  • If \(k\) and \(k'\) are kernels, so are \(k + k'\), \(kk'\), \(ck'\), …

Polynomial Kernel vs Features

\[ k_\text{poly}(\vec{x}, \vec{x}') = (\vec{x}^T\vec{x}' + c) ^ d \]

  • Primal vs Dual Optimization
  • Explicit polynomials \(\rightarrow\) compute on \(m\cdot p^d\)
  • Kernel trick \(\rightarrow\) compute on kernel matrix of shape \(m^2\)
  • For a single feature:

\[ (x^2, \sqrt{2}x, 1)^T (x'^2, \sqrt{2}x', 1) = x^2x'^2 + 2xx' + 1 = (xx' + 1)^2 \]

Poly kernels with sklearn

poly = PolynomialFeatures(include_bias=False)
X_poly = poly.fit_transform(X)
print(X.shape, X_poly.shape)
print(poly.get_feature_names())
# ((100, 2), (100, 5))
# ['x0', 'x1', 'x0^2', 'x0 x1', 'x1^2']

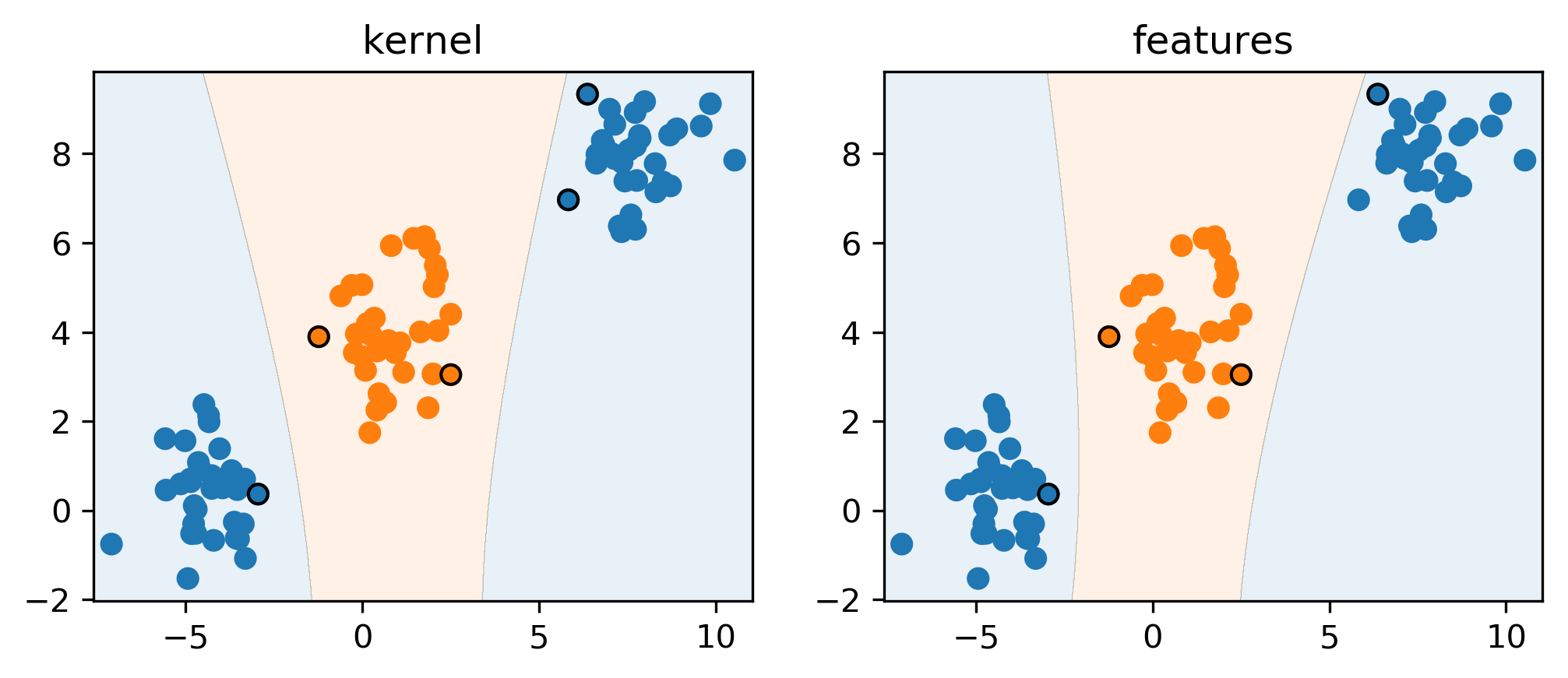
poly_kernel_features.png

Understanding Dual Coefficients

linear_svm.coef_
#array([[0.139, 0.06, -0.201, 0.048, 0.019]])

\[ y = \text{sign}(0.139 x_0 + 0.06 x_1 - 0.201 x_0^2 + 0.048 x_0 x_1 + 0.019 x_1^2) \] 

linear_svm.dual_coef_
#array([[-0.03, -0.003, 0.003, 0.03]])
linear_svm.support_
#array([1,26,42,62], dtype=int32)

\[ y = \text{sign}(-0.03 \phi(\mathbf{x}_1)^T \phi(x) - 0.003 \phi(\mathbf{x}_{26})^T \phi(\mathbf{x}) \\ +0.003 \phi(\mathbf{x}_{42})^T \phi(\mathbf{x}) + 0.03 \phi(\mathbf{x}_{62})^T \phi(\mathbf{x})) \]

With Kernel

\[y = \text{sign}\left(\summ\ai k(\xi,\vec{x})\right) \] 

poly_svm.dual_coef_
# array([[-0.057, -0. , -0.012, 0.008, 0.062]])
poly_svm.support_
# array([1,26,41,42,62], dtype=int32)

\[ y = \text{sign}(-0.057 (\vec{x}_1^T\vec{x} + 1)^2 -0.012 (\vec{x}_{41}^T \vec{x} + 1)^2 \\ +0.008 (\vec{x}_{42}^T \vec{x} + 1)^2 + 0.062 (\vec{x}_{62}^T \vec{x} + 1)^2 \]

Practical Considerations

Runtime Considerations

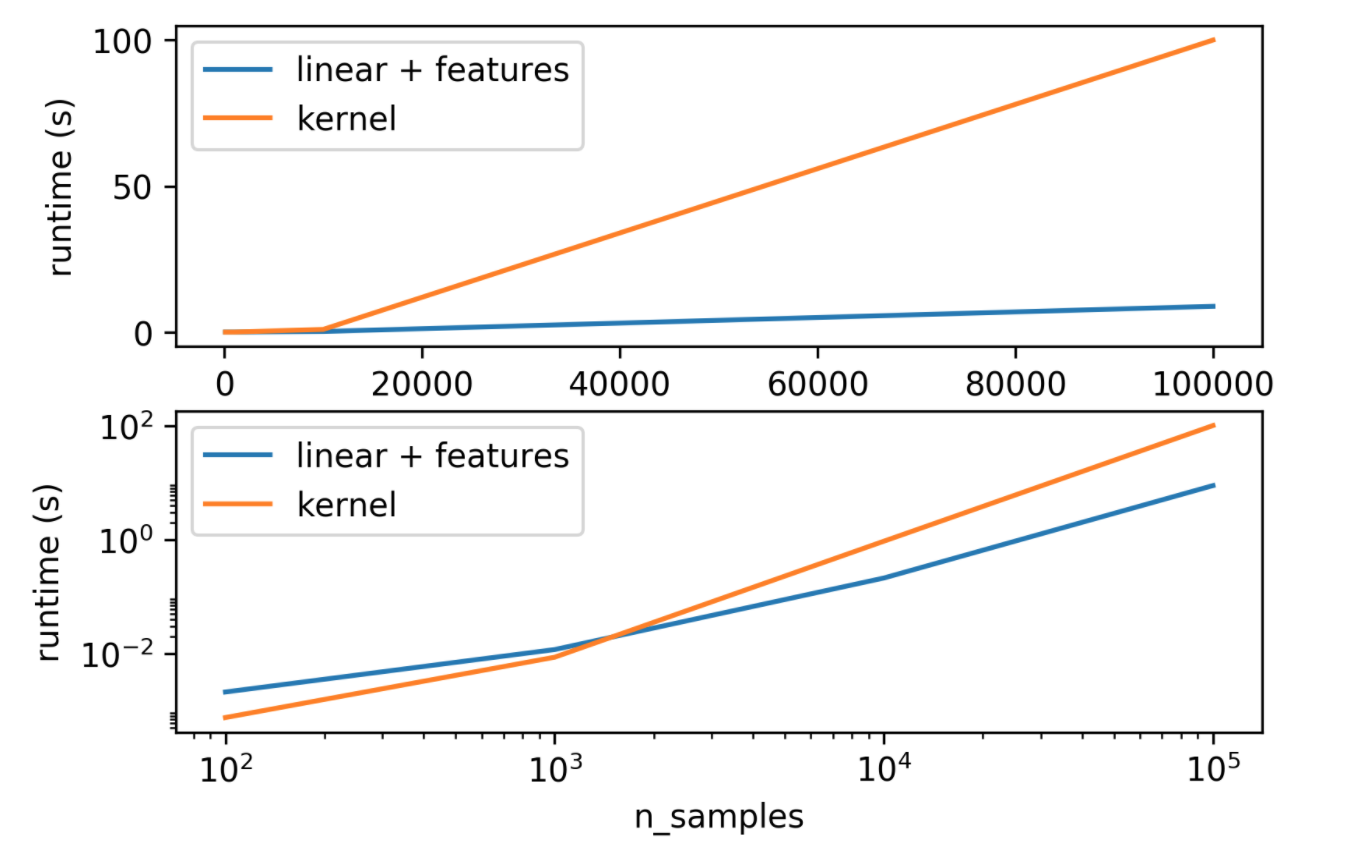
kernel_runtime.png

Kernels in Practice

  • Dual coefficients less interpretable
  • Long runtime for "large" datasets (100k samples)
  • Real power in infinite-dimensional spaces: rbf!
  • Rbf is “universal kernel” - can learn (aka overfit) anything.

Preprocessing

  • Kernel use inner products or distances.
  • Use StandardScaler or MinMaxScaler
  • Gamma parameter in RBF directly relates to scaling of data – default only works with zero-mean, unit variance.

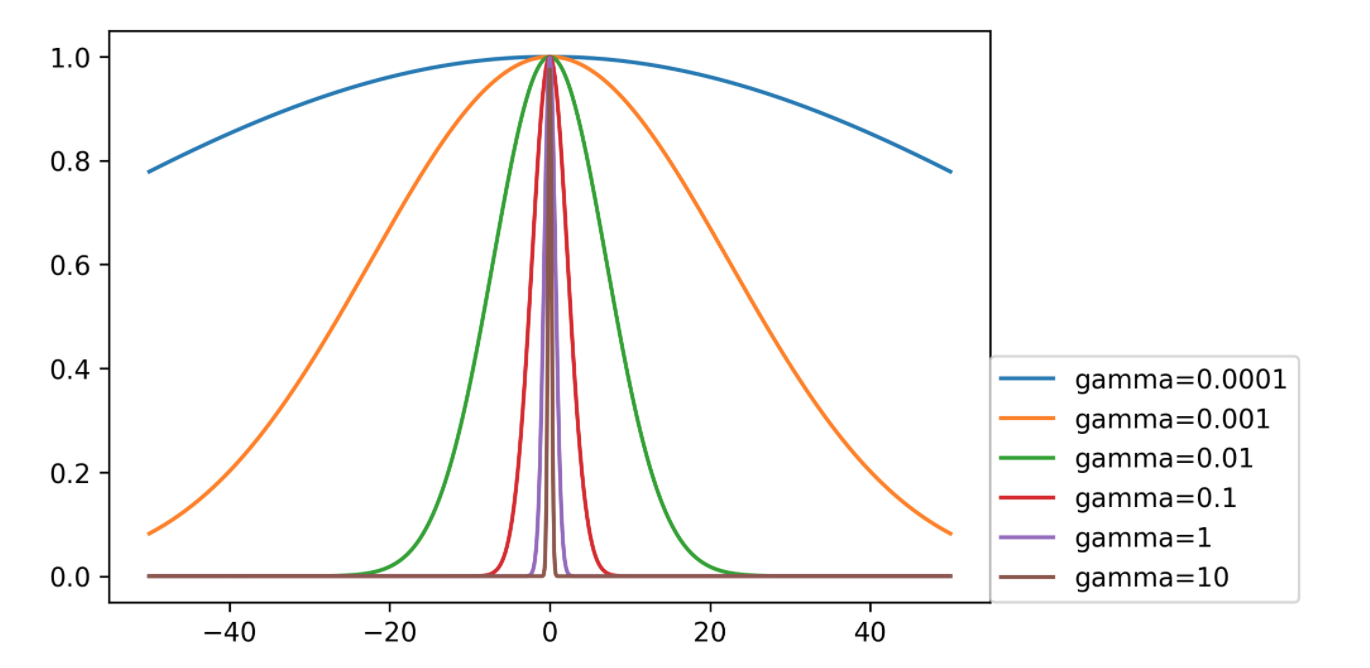
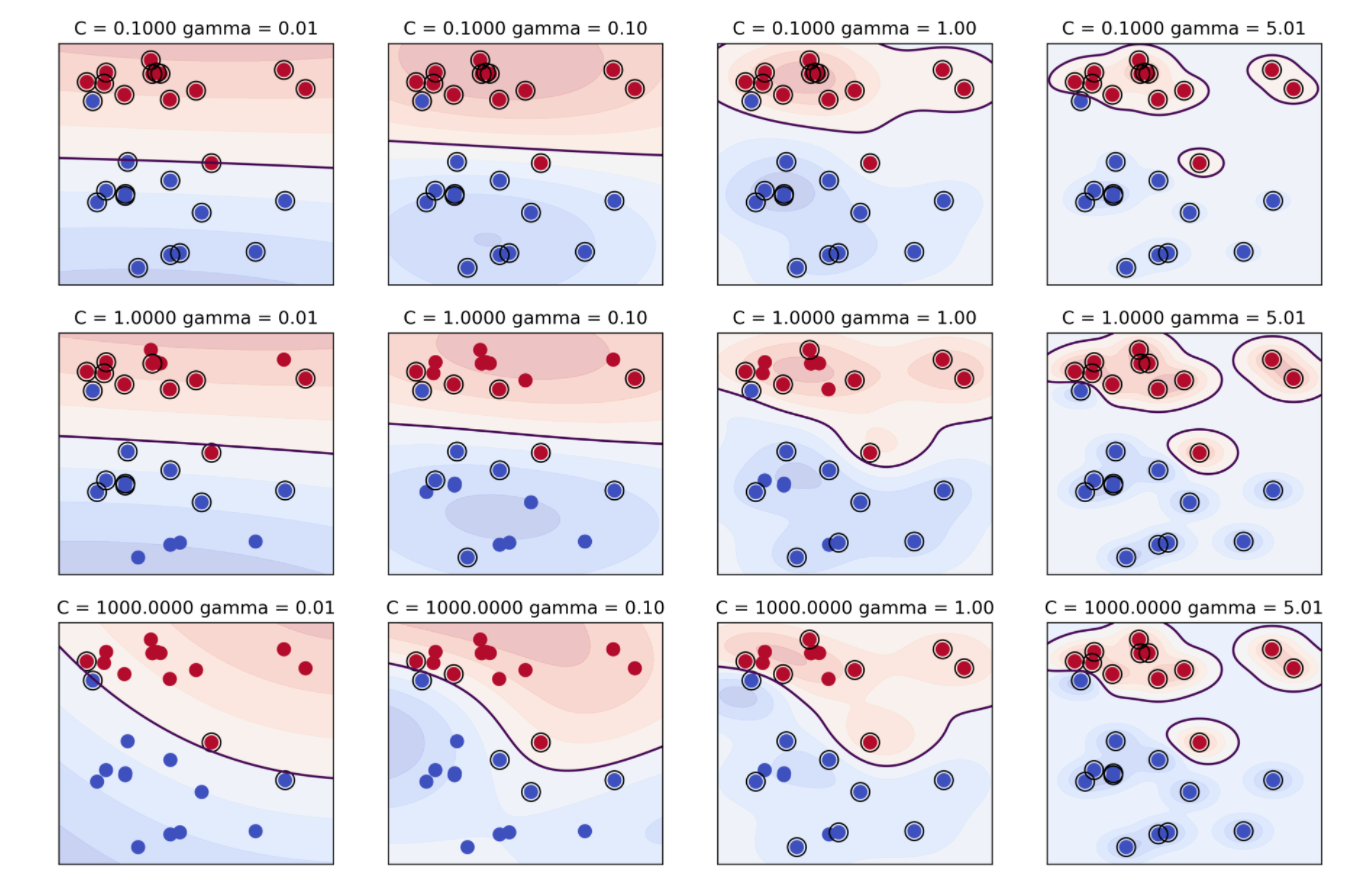
Parameters for RBF Kernels

  • Regularization parameter C is limit on alphas (for any kernel)
  • Gamma is bandwidth: \(k_\text{rbf}(\vec{x}, \vec{x}') = \exp(\gamma||\vec{x}-\vec{x}'||^2)\)

rbf_gamma.png

svm_grid.png 

from sklearn.datasets import load_digits
digits = load_digits()

digits.png

Scaling and Default Params

gamma : float, optional (default = "auto")
  Kernel coefficient for 'rbf', 'poly' and 'sigmoid'.
  If gamma is 'auto' then 1/n_features will be used

scaled_svc = make_pipeline(StandardScaler(), SVC())
print(np.mean(cross_val_score(SVC(), X_train, y_train, cv=10)))
print(np.mean(cross_val_score(scaled_svc, \
                              X_train, y_train, cv=10)))
# 0.578
# 0.978

gamma = (1. / (X_train.shape[1] * X_train.std()))
print(np.mean(cross_val_score(SVC(gamma=gamma), \
                              X_train, y_train, cv=10)))
# 0.987

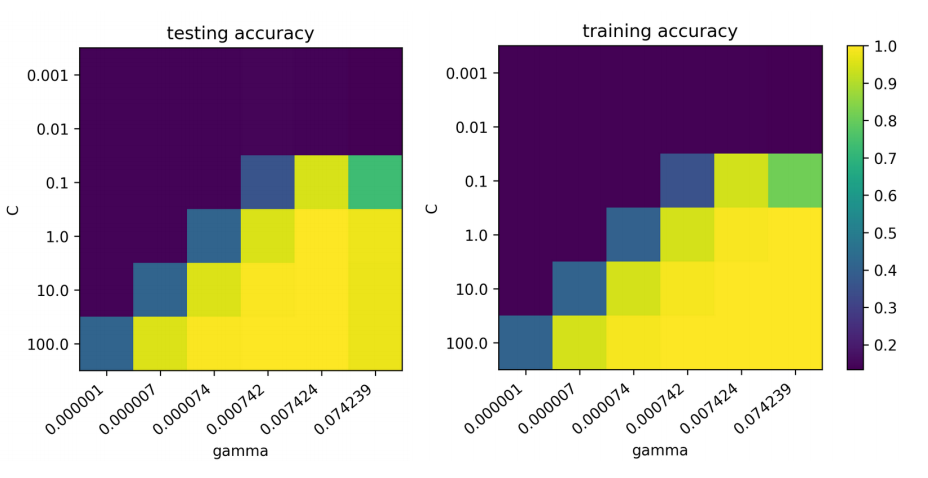
Grid-Searching Parameters

param_grid = {'svc__C': np.logspace(-3, 2, 6),
              'svc__gamma': \
              np.logspace(-3, 2, 6) / X_train.shape[0]}
param_grid

{'svc_C': array([   0.001,    0.01 ,    0.1  ,    1.   ,   10.   ,  100.   ]),
'svc_gamma': array([ 0.000001,  0.000007,  0.000074,  0.000742,  0.007424, 0.074239])}

grid = GridSearchCV(scaled_svc, param_grid=param_grid, cv=10)
grid.fit(X_train, y_train)

Grid-Searching Parameters

svm_grid_mat.png

Regression

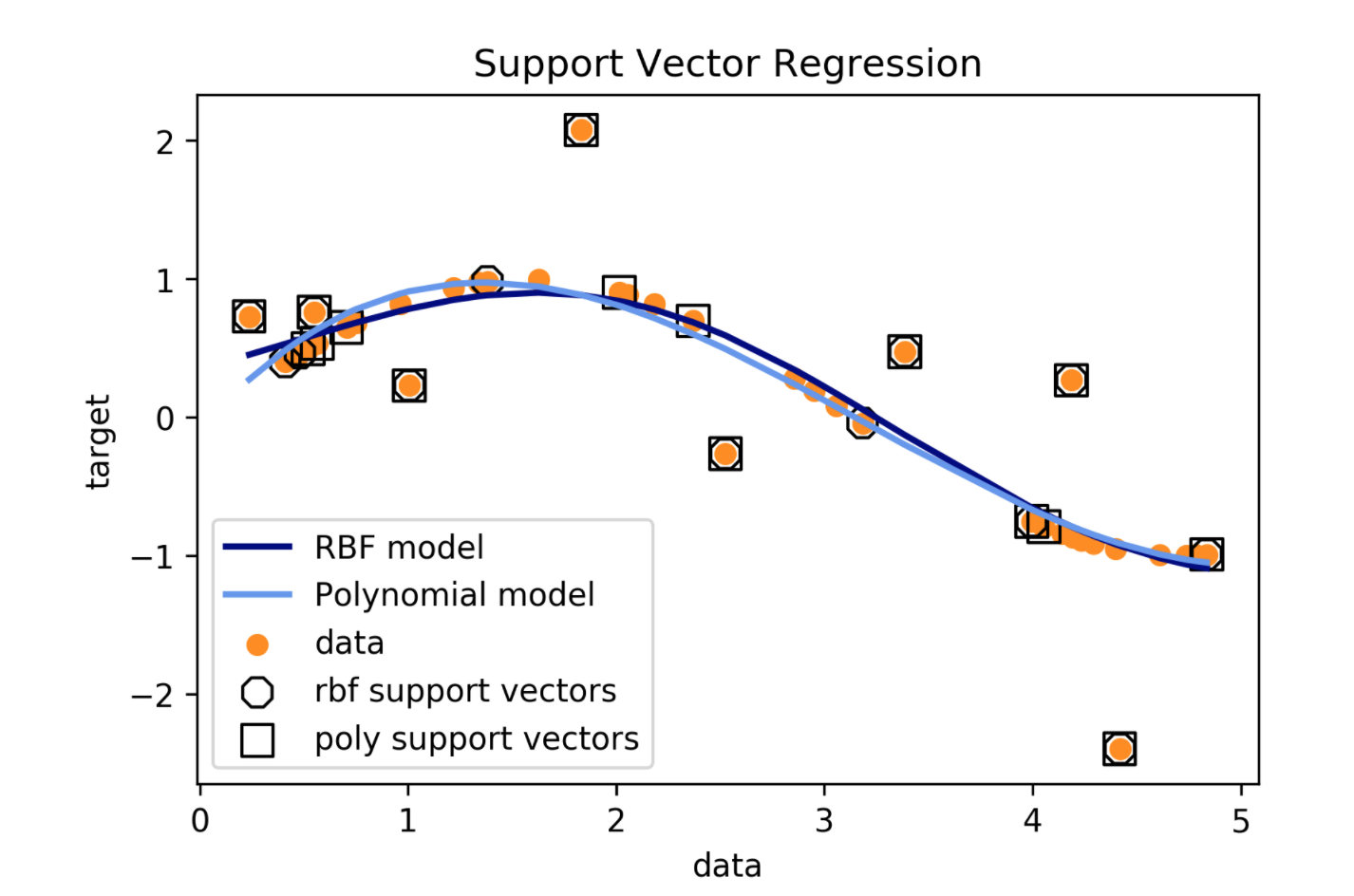
Support Vector Regression

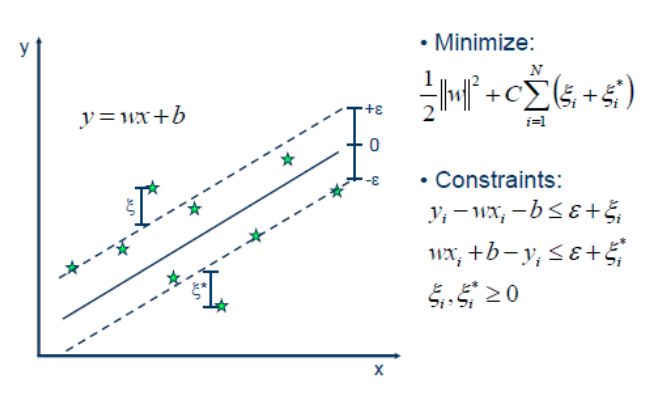
svr_math.png

Using SVR

  • Fix epsilon based on application/outliers
  • Linear kernel \(\to\) robust linear regression
  • Poly / rbf kernel \(\to\) robust non-linear regression

svr.png

Kernel Approximation

Why undo the kernel trick?

lskm.png

RKHS vs RKS

(Reproducing Kernel Hilbert-Spaces vs Random Kitchen Sinks)

  • Idea: ditch kernel, approximate (infinite-dimensional) feature map

\[\phi(x)^T \phi(x') = k(x, x') \approx \hat{\phi}(x)^T \hat{\phi}(x')\]

  • For rbf-kernel random projection followed by sin/cos , higher n_features is better

Kernel Approximation in sklearn

from sklearn.kernel_approximation import RBFSampler
gamma = 1. / (X.shape[1] * X.std())
approx_rbf = RBFSampler(gamma=gamma, n_components=5000)
print(X.shape)
X_rbf = approx_rbf.fit_transform(X)
print(X_rbf.shape)
# (1347, 64)
# (1347, 5000)
np.mean(cross_val_score(LinearSVC(), X, y, cv=10))
# 0.946
np.mean(cross_val_score(SVC(gamma=gamma), X, y, cv=10))
# 0.987
np.mean(cross_val_score(LinearSVC(), X_rbf, y, cv=10))
# 0.984

Nyström Approximation

  • Use low-rank approximation of kernel matrix
  • Select some samples, compute kernel with only those, embed all the points.
  • Using all points = full rank = exact
  • For same number of components more expensive than RBFSampler, but needs less!
from sklearn.kernel_approximation import Nystroem
nystroem = Nystroem(gamma=gamma, n_components=200)
X_train_ny = nystroem.fit_transform(X_train)
print(X_train_ny.shape)
# (1347, 200)
np.mean(cross_val_score(LinearSVC(), \
                        X_train_ny, y_train, cv=10))
# 0.974

New techniques

  • Many newer / faster algorithms out there
  • Not in sklearn so far
  • FastFood one of the most prominent ones
  • Current research on selecting good points for Nystroem.

Relation to Random Neural Nets

  • Why approximate kernels?
  • Just go random !
rng = np.random.RandomState(0)
w = rng.normal(size=(X_train.shape[1], 100))
X_train_wat = np.tanh(scale(np.dot(X_train, w)))
print(X_train_wat.shape)
# (1347, 100)

np.mean(cross_val_score(LinearSVC(), \
                        X_train_wat, y_train, cv=10))
# 0.966

Extreme Learning Machine Hoax

  • AKA random neural networks
  • Same result published in the 90s
  • Bogus math

Kernel Approximation in Practice

  • SVM: only when n_samples \(<\) 100,000 but works for n_features large
  • RBFSampler, Nystroem can allow making anything kernelized!
  • Some kernels (like chi2 and intersection) have really fast approximation.

Summary

  • Kernels are cool!
  • Kernels work best for "small" n_samples
  • Approximate kernels or random features for many samples
  • Could do even SGD / streaming with kernel approximations!